
分析 建立空間直角坐標系,設出點P的坐標為(x,y,z),則由題意可得0≤x≤1,0≤y≤1,z=1,計算$\overrightarrow{PA}$•$\overrightarrow{{PC}_{1}}$=x2-x,利用二次函數的性質求得它的值域即可.
解答  解:以點D為原點,以DA所在的直線為x軸,以DC所在的直線為y軸,以DD1所在的直線為z軸,
解:以點D為原點,以DA所在的直線為x軸,以DC所在的直線為y軸,以DD1所在的直線為z軸,
建立空間直角坐標系,如圖所示;
則點A(1,0,0),C1 (0,1,1),
設點P的坐標為(x,y,z),由題意可得 0≤x≤1,0≤y≤1,z=1;
∴$\overrightarrow{PA}$=(1-x,-y,-1),$\overrightarrow{{PC}_{1}}$=(-x,1-y,0),
∴$\overrightarrow{PA}$•$\overrightarrow{{PC}_{1}}$=-x(1-x)-y(1-y)+0=x2-x+y2-y=${(x-\frac{1}{2})}^{2}$+${(y-\frac{1}{2})}^{2}$-$\frac{1}{2}$,
由二次函數的性質可得,當x=y=$\frac{1}{2}$時,$\overrightarrow{PA}$•$\overrightarrow{{PC}_{1}}$取得最小值為-$\frac{1}{2}$;
當x=0或1,且y=0或1時,$\overrightarrow{PA}$•$\overrightarrow{{PC}_{1}}$取得最大值為0,
則$\overrightarrow{PA}$•$\overrightarrow{{PC}_{1}}$的取值范圍是[-$\frac{1}{2}$,0].
故答案為:[-$\frac{1}{2}$,0].
點評 本題主要考查了向量在幾何中的應用與向量的數量積運算問題,是綜合性題目.


 沖刺100分1號卷系列答案
沖刺100分1號卷系列答案 期末好成績系列答案
期末好成績系列答案科目:高中數學 來源: 題型:選擇題
| A. | f(0)<f(3)<f(5) | B. | f(0)<f(5)<f(3) | C. | f(5)<f(3)<f(0) | D. | f(5)<f(0)<f(3) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
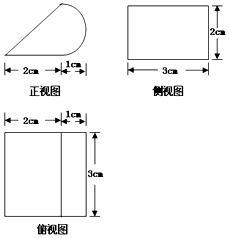
| A. | (19+π)cm2 | B. | (22+4π)cm2 | C. | (10+6$\sqrt{2}$+4π)cm2 | D. | (13+6$\sqrt{2}$+4π)cm2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{1}$=1 | B. | $\frac{{x}^{2}}{1}$-$\frac{{y}^{2}}{3}$=1 | C. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{1}$=1 | D. | $\frac{{x}^{2}}{1}$-$\frac{{y}^{2}}{9}$=1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 若a<-1,則x+a<1nx | B. | 若a≥-1,則x+a<1nx | ||
| C. | 若a<-1,則x+a≥1nx | D. | 若a≥-1,則x+a≤1nx |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com