Question

【題目】點O為坐標原點，直線l經過拋物線C：y2=4x的焦點F．
（Ⅰ）若點O到直線l的距離為 ， 求直線l的方程；
（Ⅱ）設點A是直線l與拋物線C在第一象限的交點．點B是以點F為圓心，|FA|為半徑的圓與x軸負半軸的交點．試判斷直線AB與拋物線C的位置關系，并給出證明．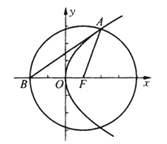

Answer 1

【答案】解法一：（Ⅰ）拋物線的焦點F（1，0），
當直線l的斜率不存在時，即x=1不符合題意．
當直線l的斜率存在時，
設直線l的方程為：y=k（x﹣1），即kx﹣y﹣k=0．
所以，，解得：．
故直線l的方程為：y=(x-1)，即
（Ⅱ）直線AB與拋物線相切，證明如下：
（法一）：設A（x0 ， y0），則．
因為|BF|=|AF|=x0+1，所以B（﹣x0 ， 0）．
所以直線AB的方程為：y=，
整理得：x=…（1）
把方程（1）代入y2=4x得：，
，
所以直線AB與拋物線相切．
【解析】（Ⅰ）拋物線的焦點F（1，0），當直線l的斜率不存在時，即x=1不符合題意．當直線l的斜率存在時，設直線l的方程為：y=k（x﹣1），所以 ， 由此能求出直線l的方程．
（Ⅱ）直線AB與拋物線相切．設A（x0 ， y0），則 ． 因為|BF|=|AF|=x0+1，所以B（﹣x0 ， 0），由此能夠證明直線AB與拋物線相切．