
【題目】據市場調查發現,某種產品在投放市場的30天中,其銷售價格![]() (元)和時間
(元)和時間![]() (天)的關系如圖所示.
(天)的關系如圖所示.

(1)求銷售價格![]() (元)和時間
(元)和時間![]() (天)的函數關系式;
(天)的函數關系式;
(2)若日銷售量![]() (件)與時間
(件)與時間![]() (天)的函數關系式是
(天)的函數關系式是![]()
![]() ,問該產品投放市場第幾天時,日銷售額
,問該產品投放市場第幾天時,日銷售額![]() (元)最高,且最高為多少元?
(元)最高,且最高為多少元?
【答案】(Ⅰ)![]() ;(Ⅱ)在第10天時,日銷售額最大,最大值為900元.
;(Ⅱ)在第10天時,日銷售額最大,最大值為900元.
【解析】
試題(Ⅰ)通過討論t的范圍,求出函數的表達式即可;(Ⅱ)先求出函數的表達式,通過討論t的范圍,求出函數的最大值即可.
解:(Ⅰ)①當0≤t<20,t∈N時,
設P=at+b,將(0,20),(20,40)代入,得![]() 解得
解得![]()
所以P=t+20(0≤t<20,t∈N).
②當20≤t≤30,t∈N時,
設P=at+b,將(20,40),(30,30)代入,解得![]()
所以 P=﹣t+60(20≤t≤30,t∈N),)
綜上所述![]()
(Ⅱ)依題意,有y=PQ,
得![]()
化簡得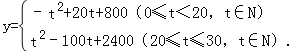
整理得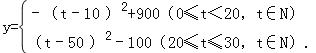
①當0≤t<20,t∈N時,由y=﹣(t﹣10)2+900可得,當t=10時,y有最大值900元.
②當20≤t≤30,t∈N時,由y=(t﹣50)2﹣100可得,當t=20時,y有最大值800元.
因為 900>800,所以在第10天時,日銷售額最大,最大值為900元.


科目:高中數學 來源: 題型:
【題目】在△ABC中,內角A、B、C所對的邊分別為a、b、c,已知a≠b,cos2A﹣cos2B= ![]() sinAcosA﹣
sinAcosA﹣ ![]() sinBcosB. (Ⅰ)求角C的大小;
sinBcosB. (Ⅰ)求角C的大小;
(Ⅱ)若c= ![]() ,siniA=
,siniA= ![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某鄉鎮為了提高當地地方經濟總量,決定引進資金對原有的兩個企業![]() 和
和![]() 進行改造,計劃每年對兩個企業共投資500萬元,要求對每個企業至少投資50萬元.根據已有經驗,改造后
進行改造,計劃每年對兩個企業共投資500萬元,要求對每個企業至少投資50萬元.根據已有經驗,改造后![]() 企業的年收益
企業的年收益![]() (單位:萬元)和
(單位:萬元)和![]() 企業的年收益
企業的年收益![]() (單位:萬元)與投入資金
(單位:萬元)與投入資金![]() (單位:萬元)分別滿足關系式:
(單位:萬元)分別滿足關系式:![]() ,
,![]() .設對
.設對![]() 企業投資額為
企業投資額為![]() (單位:萬元),每年兩個企業的總收益為
(單位:萬元),每年兩個企業的總收益為![]() (單位:萬元).
(單位:萬元).
(1)求![]() ;
;
(2)試問如何安排兩個企業的投入資金,才能使兩個企業的年總收益達到最大,并求出最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足a1=1,an+1=2an+1(n∈N*).
(1)求數列{an}的通項公式;
(2)設Sn為數列{ ![]() }的前n項和,求證:1≤Sn<4.
}的前n項和,求證:1≤Sn<4.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (k為常數,e為自然對數的底數),曲線
(k為常數,e為自然對數的底數),曲線![]() 在點(1, f (1))處的切線與x軸平行.
在點(1, f (1))處的切線與x軸平行.
(1)求k的值;
(2)求![]() 的單調區間;
的單調區間;
(3)設![]() 其中
其中![]() 為
為![]() 的導函數,證明:對任意
的導函數,證明:對任意![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】古希臘亞歷山大時期的數學家帕普斯(Pappus,約300~約350)在《數學匯編》第3卷中記載著一個定理:“如果同一平面內的一個閉合圖形的內部與一條直線不相交,那么該閉合圖形圍繞這條直線旋轉一周所得到的旋轉體的體積等于閉合圖形面積乘以重心旋轉所得周長的積.”如圖,半圓![]() 的直徑
的直徑![]() ,點
,點![]() 是該半圓弧的中點,半圓弧與直徑
是該半圓弧的中點,半圓弧與直徑![]() 所圍成的半圓面(陰影部分不含邊界)的重心
所圍成的半圓面(陰影部分不含邊界)的重心![]() 位于對稱軸
位于對稱軸![]() 上.若半圓面繞直徑
上.若半圓面繞直徑![]() 所在直線旋轉一周,則所得到的旋轉體的體積為__________
所在直線旋轉一周,則所得到的旋轉體的體積為__________![]() ,
,![]() ___________________
___________________![]() .
.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com