
【題目】已知點![]() 在橢圓
在橢圓![]() 上,
上,![]() 、
、![]() 分別為
分別為![]() 的左、右頂點,直線
的左、右頂點,直線![]() 與
與![]() 的斜率之積為
的斜率之積為![]() ,
,![]() 為橢圓的右焦點,直線
為橢圓的右焦點,直線![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)直線![]() 過點
過點![]() 且與橢圓
且與橢圓![]() 交于
交于![]() 、
、![]() 兩點,直線
兩點,直線![]() 、
、![]() 分別與直線
分別與直線![]() 交于
交于![]() 、
、![]() 兩點.試問:以
兩點.試問:以![]() 為直徑的圓是否過定點?如果是,求出定點坐標,否則,請說明理由.
為直徑的圓是否過定點?如果是,求出定點坐標,否則,請說明理由.
【答案】(1)![]() ;(2)過定點
;(2)過定點![]() 和
和![]() ,理由見解析.
,理由見解析.
【解析】
(1)利用直線![]() 與
與![]() 的斜率之積為
的斜率之積為![]() ,得出
,得出![]() ,再由點
,再由點![]() 在橢圓上,可求出
在橢圓上,可求出![]() 的值,即可得出橢圓
的值,即可得出橢圓![]() 的標準方程;
的標準方程;
(2)由對稱性知,以![]() 為直徑的圓過
為直徑的圓過![]() 軸上的定點
軸上的定點![]() ,設直線
,設直線![]() 的方程為
的方程為![]() ,點
,點![]() 、
、![]() ,設點
,設點![]() 、
、![]() ,求出
,求出![]() 、
、![]() ,將直線
,將直線![]() 的方程與橢圓
的方程與橢圓![]() 的方程聯立,列出韋達定理,求出
的方程聯立,列出韋達定理,求出![]() 的值,由
的值,由![]() ,結合韋達定理求出
,結合韋達定理求出![]() 的值,即可得出定點
的值,即可得出定點![]() 的坐標.
的坐標.
(1)![]() 點
點![]() 在橢圓
在橢圓![]() 上,則
上,則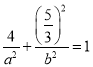 ,①,
,①,
易知點![]() 、
、![]() ,
,
直線![]() 的斜率為
的斜率為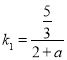 ,直線
,直線![]() 的斜率為
的斜率為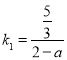 ,
,
由題意可得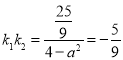 ,解得
,解得![]() ,代入①式得
,代入①式得![]() ,
,
因此,橢圓![]() 的方程為
的方程為![]() ;
;
(2)易知,直線![]() 不能與
不能與![]() 軸重合.
軸重合.
由對稱性知,以![]() 為直徑的圓過
為直徑的圓過![]() 軸上的定點
軸上的定點![]() ,
,
設直線![]() 的方程為
的方程為![]() ,點
,點![]() 、
、![]() ,設點
,設點![]() 、
、![]() ,
,
如下圖所示:
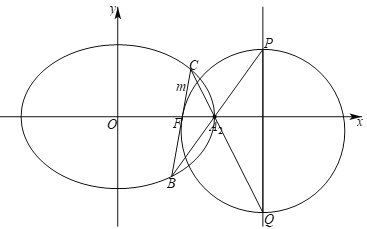
易知點![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,
得![]() ,同理可得
,同理可得![]() .
.
將直線![]() 的方程與橢圓
的方程與橢圓![]() 的方程聯立
的方程聯立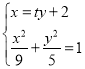 ,
,
消去![]() 得,
得,![]() ,
,![]() .
.
由韋達定理得![]() ,
,![]() ,
,
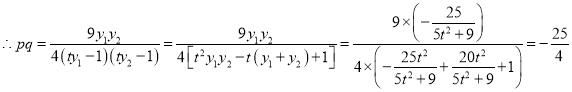 ,
,
![]() ,
,![]() ,
,
![]() ,解得
,解得![]() 或
或![]() .
.
因此,以![]() 為直徑的圓過定點
為直徑的圓過定點![]() 和
和![]() .
.


 特高級教師點撥系列答案
特高級教師點撥系列答案 文敬圖書課時先鋒系列答案
文敬圖書課時先鋒系列答案科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).以坐標原點
為參數).以坐標原點![]() 為極點,
為極點,![]() 軸的非負半軸建立極坐標系,點
軸的非負半軸建立極坐標系,點![]() 的極坐標
的極坐標![]() ,曲線
,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若![]() 為曲線
為曲線![]() 上的動點,求
上的動點,求![]() 中點
中點![]() 到直線
到直線![]() 的距離最小值.
的距離最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,點
中,點![]() ,
,![]() 是曲線
是曲線![]() 上的任意一點,動點
上的任意一點,動點![]() 滿足
滿足![]()
(1)求點![]() 的軌跡方程;
的軌跡方程;
(2)經過點![]() 的動直線
的動直線![]() 與點
與點![]() 的軌跡方程交于
的軌跡方程交于![]() 兩點,在
兩點,在![]() 軸上是否存在定點
軸上是否存在定點![]() (異于點
(異于點![]() ),使得
),使得![]() ?若存在,求出
?若存在,求出![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某小區有一塊三角形空地,如圖△ABC,其中AC=180米,BC=90米,∠C=90°,開發商計劃在這片空地上進行綠化和修建運動場所,在△ABC內的P點處有一服務站(其大小可忽略不計),開發商打算在AC邊上選一點D,然后過點P和點D畫一分界線與邊AB相交于點E,在△ADE區域內綠化,在四邊形BCDE區域內修建運動場所. 現已知點P處的服務站與AC距離為10米,與BC距離為100米. 設![]() 米,試問
米,試問![]() 取何值時,運動場所面積最大?
取何值時,運動場所面積最大?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列關于充分必要條件的判斷中,錯誤的是( )
A.“![]() ”是“
”是“![]() ”的充分條件
”的充分條件
B.“![]() ”是“
”是“![]() ”的必要條件
”的必要條件
C.“![]() ”是“
”是“![]() ”的充要條件
”的充要條件
D.“![]() ,
,![]() ”是“
”是“![]() ”的非充分非必要條件
”的非充分非必要條件
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com