Question

13．在直角坐標系xOy中，設(shè)圓的方程為（x+2$\sqrt{2}$）²+y²=48，F(xiàn)₁是圓心，F(xiàn)₂（2$\sqrt{2}$，0）是圓內(nèi)一點，E為圓周上任一點，線EF₂的垂直平分線EF₁的連線交于P點，設(shè)動點P的軌跡為曲線C．
（Ⅰ）求曲線C的方程；
（Ⅱ）設(shè)直線l（與x軸不重合）與曲線C交于A、B兩點，與x軸交于點M．
      （i）是否存在定點M，使得$\frac{1}{|MA{|}^{2}}$+$\frac{1}{|MB{|}^{2}}$為定值，若存在，求出點M坐標及定值；若不存在，請說明理由；
      （ii）在滿足（i）的條件下，連接并延長AO交曲線C于點Q，試求△ABQ面積的最大值．

Answer 1

分析 （Ⅰ）由足$P{F}_{1}+P{F}_{2}=E{F}_{2}=4\sqrt{3}$，且4$\sqrt{3}$＞丨F₁F₂丨，則點P的軌跡為以F₁、F₂為焦點，長軸為4$\sqrt{3}$的橢圓，即可求得橢圓方程；
（Ⅱ）（i）設(shè)直線l的方程，代入橢圓方程，由$\frac{1}{丨MA{丨}^{2}}$+$\frac{1}{丨MB{丨}^{2}}$=$\frac{（{y}_{1}+{y}_{2}）^{2}-2{y}_{1}{y}_{2}}{（{m}^{2}+1）（{y}_{1}{y}_{2}）^{2}}$，利用韋達定理可知2t²+24=72-6t²，即可求得t的值，$\frac{1}{丨MA{丨}^{2}}$+$\frac{1}{丨MB{丨}^{2}}$=1；
（ii）利用弦長公式，求得丨AB丨，利用點到直線距離公式，換元，即可求得△ABQ面積的最大值．

解答 解：（Ⅰ）∵圓的方程為（x+2$\sqrt{2}$）²+y²=48的圓心F₁為（-2$\sqrt{2}$，0），半徑為4$\sqrt{3}$．
依題意點P滿足$P{F}_{1}+P{F}_{2}=E{F}_{2}=4\sqrt{3}$，且4$\sqrt{3}$＞丨F₁F₂丨，
故點P的軌跡為以F₁、F₂為焦點，長軸為4$\sqrt{3}$的橢圓
∴曲線C的方程：$\frac{{x}^{2}}{12}+\frac{{y}^{2}}{4}=1$．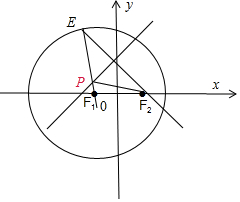

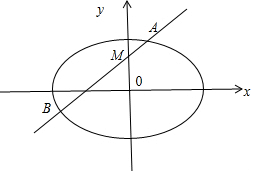
（Ⅱ）（i）設(shè)M（t，0），設(shè)直線l的方程：x=my+t，A（x₁，y₁），B（x₂，y₂），
聯(lián)立$\left\{\begin{array}{l}{x=my+t}\\{{x}^{2}+3{y}^{2}=12}\end{array}\right.$，整理得：（m²+3）y²+2mty+t²-12=0，
y₁+y₂=-$\frac{2mt}{{m}^{2}+3}$，y₁y₂=$\frac{{t}^{2}-12}{{m}^{2}+3}$，
$\frac{1}{丨MA{丨}^{2}}$=$\frac{1}{（{m}^{2}+1）{y}_{1}^{2}}$，$\frac{1}{丨MB{丨}^{2}}$=$\frac{1}{（{m}^{2}+1）{y}_{2}^{2}}$，
則$\frac{1}{丨MA{丨}^{2}}$+$\frac{1}{丨MB{丨}^{2}}$=$\frac{（{y}_{1}+{y}_{2}）^{2}-2{y}_{1}{y}_{2}}{（{m}^{2}+1）（{y}_{1}{y}_{2}）^{2}}$=$\frac{（2{t}^{2}+24）{m}^{2}+72-6{t}^{2}}{（{t}^{2}-12）{m}^{2}+（{t}^{2}-12）^{2}}$，
當2t²+24=72-6t²，即t²=6時，$\frac{1}{丨MA{丨}^{2}}$+$\frac{1}{丨MB{丨}^{2}}$=1，
此時M的坐標為（±$\sqrt{6}$，0），
綜上，存在點M（±$\sqrt{6}$，0），使得$\frac{1}{丨MA{丨}^{2}}$+$\frac{1}{丨MB{丨}^{2}}$=1，
（ii）由（i）可知：t²=6，則丨AB丨=$\sqrt{1+{m}^{2}}$丨y₁-y₂丨=$\sqrt{1+{m}^{2}}$$\frac{2\sqrt{6}\sqrt{2{m}^{2}+3}}{{m}^{2}+3}$，
原點O直線AB的距離d=$\frac{\sqrt{6}}{\sqrt{1+{m}^{2}}}$，S_△ABQ=4×$\frac{1}{2}$×$\frac{丨AB丨}{2}$=$\frac{12\sqrt{2{m}^{2}+3}}{{m}^{2}+3}$，
令$\sqrt{2{m}^{2}+3}$=μ∈[$\sqrt{3}$，+∞），則S_△ABQ=$\frac{24μ}{{u}^{2}+3}$=$\frac{24}{μ+\frac{3}{μ}}$≤$\frac{24}{2\sqrt{3}}$=4$\sqrt{3}$，
當且僅當t=$\sqrt{3}$，即m=0取最大值，
∴△ABQ面積的最大值4$\sqrt{3}$．

點評 本題考查橢圓的標準方程，直線與橢圓的位置關(guān)系，考查韋達定理，弦長公式，考查換元法的應(yīng)用，考查計算能力，屬于中檔題．