
分析 根據解析式對a分類討論,分別列出不等式后,由指數、對數函數的性質求出實數a的取值范圍.
解答 解:由題意知,f(x)=$\left\{\begin{array}{l}{{2}^{1-x},x≤0}\\{1-lo{g}_{2}x,x>0}\end{array}\right.$,
①當a≤0時,不等式|f(a)|≥2為|21-a|≥2,
則21-a≥2,即1-a≥1,解得a≤0;
②當a>0時,不等式|f(a)|≥2為$|1-lo{g}_{2}^{a}|≥2$,
則$1-lo{g}_{2}^{a}≥2$或$1-lo{g}_{2}^{a}≤-2$,
即$lo{g}_{2}^{a}≤-1$或$lo{g}_{2}^{a}≥3$,解得0<a $≤\frac{1}{2}$或a≥8;
綜上可得,實數a的取值范圍是$(-∞,\frac{1}{2}]∪[8,+∞)$,
故答案為:$(-∞,\frac{1}{2}]∪[8,+∞)$.
點評 本題考查利用分段函數求不等式的解集,以及指數、對數函數的性質的應用,考查分類討論思想,化簡、變形能力.


 每課必練系列答案
每課必練系列答案科目:高中數學 來源: 題型:解答題
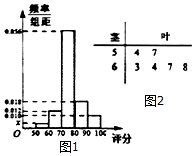 某單位為了解甲、乙兩部門對本單位職工的服務情況,隨機訪問50名職工.已知50名職工對甲、乙兩部門的評分都在區間[50,100]內,根據50名職工對甲部門的評分繪制的頻率分布直方圖,以及根據50名職工對乙部門評分中落在[50,60),[60,70)內的所有數據繪制的莖葉圖,如圖所示.
某單位為了解甲、乙兩部門對本單位職工的服務情況,隨機訪問50名職工.已知50名職工對甲、乙兩部門的評分都在區間[50,100]內,根據50名職工對甲部門的評分繪制的頻率分布直方圖,以及根據50名職工對乙部門評分中落在[50,60),[60,70)內的所有數據繪制的莖葉圖,如圖所示.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
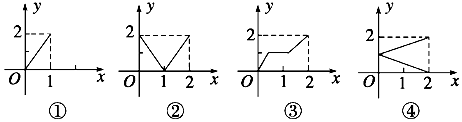
| A. | ①②③④ | B. | ①②③ | C. | ②③ | D. | ② |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 13 | C. | 4或10 | D. | 1或13 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 第四象限 | B. | 第一象限 | C. | 第三象限 | D. | 第二象限 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 4x-5y+7=0 | B. | 5x-4y+11=0 | C. | 2x-3y-4=0 | D. | 4x+5y-23=0 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com