
分析 (1)根據題意,由f(a+2)=81可得3a+2=81,解可得a的值,即可得函數g(x)的解析式,結合g(x)的解析式,先分析其定義域,再分析g(-x)與g(x)的關系,即可得答案;
(2)由(1)得到g(x)的解析式,將其變形可得g(x)=$\frac{2}{1+{2}^{x}}$-1,結合指數函數的性質分析即可得答案.
解答 解:(1)由f(a+2)=3a+2=81,得a+2=4,故a=2;
所以$g(x)=\frac{{1-{2^x}}}{{1+{2^x}}}$;
對于$g(x)=\frac{{1-{2^x}}}{{1+{2^x}}}$,其定義域為R,
而又由$g({-x})=\frac{{1-{2^{-x}}}}{{1+{2^{-x}}}}=\frac{{{2^x}-1}}{{{2^x}+1}}=-\frac{{1-{2^x}}}{{{2^x}+1}}=-g(x)$,
所以函數g(x)為奇函數;
(2)$g(x)=\frac{{1-{2^x}}}{{1+{2^x}}}=\frac{{2-(1+{2^x})}}{{1+{2^x}}}=\frac{2}{{1+{2^x}}}-1$,
${2^x}∈(0,+∞)⇒{2^x}+1∈(1,+∞)⇒\frac{1}{{{2^x}+1}}∈(0,1)$,
所以$\frac{2}{{{2^x}+1}}$$∈(0,2)⇒\frac{2}{{1+{2^x}}}-1∈(-1,1)$,
即函數g(x)的值域為(-1,1).
點評 本題考查函數的單調性、奇偶性的判定與應用,判定奇偶性之前要先分析函數的定義域.


 陽光考場單元測試卷系列答案
陽光考場單元測試卷系列答案 名校聯盟沖刺卷系列答案
名校聯盟沖刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{20}$ | |
| B. | $\frac{50}{1002}$ | |
| C. | $\frac{1}{1001}$ | |
| D. | 有兩個個體與其它個體被抽到的概率不相等 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
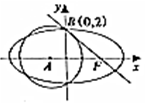 如圖,點F為橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)右焦點,圓A:(x-t)2+y2=$\frac{16}{3}$(t<0)與橢圓C的一個公共點為B(0,2),且直線FB與圓A相切于點B.
如圖,點F為橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)右焦點,圓A:(x-t)2+y2=$\frac{16}{3}$(t<0)與橢圓C的一個公共點為B(0,2),且直線FB與圓A相切于點B.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 18 | B. | 3 | C. | 15 | D. | 9 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
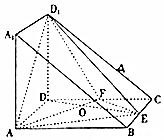 將棱長為2的正方體沿對角A1BAD1截去一半得到如圖所示的幾何體,點E,F分別是BC,DC的中點,AF與DE相交于O點.
將棱長為2的正方體沿對角A1BAD1截去一半得到如圖所示的幾何體,點E,F分別是BC,DC的中點,AF與DE相交于O點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com