
| 選考物理、化學、生物的科目數 | 1 | 2 | 3 |
| 人數 | 5 | 25 | 20 |
分析 (Ⅰ)計算“所選取的2名學生選考物理、化學、生物科目數量相等”為事件A,利用對立事件的概率公式計算選考物理、化學、生物科目數量不相等的概率值;
(Ⅱ)由題意知X的可能取值,計算對應的概率值,寫出X的分布列,計算數學期望值;
(Ⅲ)計算所調查的50名學生中物理、化學、生物選考兩科目的學生人數,求出相應的頻率,根據n次獨立重復實驗恰有k次發生的概率,求出對應的概率值.
解答 解:(Ⅰ)記“所選取的2名學生選考物理、化學、生物科目數量相等”為事件A,
則$P(A)=\frac{{C_5^2+C_{25}^2+C_{20}^2}}{{C_{50}^2}}=\frac{20}{49}$,
所以他們選考物理、化學、生物科目數量不相等的概率為
$1-P(A)=\frac{29}{49}$;…(3分)
(Ⅱ)由題意可知X的可能取值分別為0,1,2;
則.$P(X=0)=\frac{{C_5^2+C_{25}^2+C_{20}^2}}{{C_{50}^2}}=\frac{20}{49}$,
$P(X=1)=\frac{{C_5^1C_{25}^1+C_{20}^1C_{25}^1}}{{C_{50}^2}}=\frac{25}{49}$,
$P(X=2)=\frac{{C_5^1C_{20}^1}}{{C_{50}^2}}=\frac{4}{49}$;…(6分)
從而X的分布列為:
| X | 0 | 1 | 2 |
| p | $\frac{20}{49}$ | $\frac{25}{49}$ | $\frac{4}{49}$ |
點評 本題考查了離散型隨機變量的分布列與數學期望的計算問題,是中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | 當a>1時,函數y=ax是增函數,因為2>1,所以函數y=2x是增函數,這種推理是合情推理 | |
| B. | 在平面中,對于三條不同的直線a,b,c,若a∥b,b∥c,則a∥c,將此結論放到空間中也是如此.這種推理是演繹推理 | |
| C. | 命題$P:?{x_0}∈R,{e^{x_0}}<{x_0}$的否定是¬P:?x∈R,ex>x | |
| D. | 若分類變量X與Y的隨機變量K2的觀測值k越小,則兩個分類變量有關系的把握性越小 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
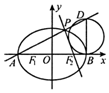 已知橢圓C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的離心率為$\frac{1}{2}$,左、右焦點為F1,F2,點M為橢圓C上的任意一點,$\overrightarrow{M{F_1}}•\overrightarrow{M{F_2}}$的最小值為2.
已知橢圓C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的離心率為$\frac{1}{2}$,左、右焦點為F1,F2,點M為橢圓C上的任意一點,$\overrightarrow{M{F_1}}•\overrightarrow{M{F_2}}$的最小值為2.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(x)=2x2-8x+11 | B. | f(x)=-2x2+8x-1 | C. | f(x)=2x2-4x+3 | D. | f(x)=-2x2+4x+3 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $±\frac{3}{5}$ | D. | $±\frac{4}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-2,-1) | B. | [-2,-1) | C. | (-2,+∞) | D. | [-2,+∞) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com