
分析 (1)利用數列遞推式,n分別取1,2,3,代入計算,即可得到結論;
(2)令Sn=a1+a2+…+an,Sn2=a13+a23+…+an3(n∈N*).可得再寫一式,兩式相減,可得數列{an}的任一項an與它的前一項an-1間的遞推關系;利用a1=1,a2017=-2016,所以無窮數列{an}的前2016項組成首項和公差均為1的等差數列,從第2016項開始組成首項為-2016,公比為-1的等比數列,從而可得數列的通項.
(3)根據遞推式得出An的所有元素規律,利用歸納法得出結論.
解答 解:(1)當n=1時,a13=a12,由a1≠0得a1=1.
當n=2時,1+a23=(1+a2)2,由a2≠0得a2=2或a2=-1.
當n=3時,1+a23+a33=(1+a2+a3)2,若a2=2得a3=3或a3=-2;若a2=-1得a3=1;
綜上討論,滿足條件的數列有三個:1,2,3或1,2,-2或1,-1,1.
(2)令Sn=a1+a2+…+an,則Sn2=a13+a23+…+an3(n∈N*).
從而(Sn+an+1)2=a13+a23+…+an3+an+13,
兩式相減,結合an+1≠0,得2Sn=an+12-an+1.
當n=1時,由(1)知a1=1;
當n≥2時,2an=2(Sn-Sn-1)=(an+12-an+1)-(an2-an),即(an+1+an)(an+1-an-1)=0,
所以an+1=-an或an+1=an+1.
又a1=1,a2017=-2016,所以無窮數列{an}的前2016項組成首項和公差均為1的等差數列,從第2016項開始組成首項為-2016,公比為-1的等比數列.
an=$\left\{\begin{array}{l}{n,1≤n≤2016}\\{(-1)^{n}•2016,n>2016}\end{array}\right.$.
(3)由(2)可知a1=1,an=-an-1或an=an-1+1(n≥2),
故A1={1},A2={-1,2},A3={1,-2,3},A4={-1,2,-3,4},…
∴當n為奇數時,An的所有元素之和為1+3+5+…+n-(2+4+6+…n-1)=$\frac{1+n}{2}•\frac{n+1}{2}$-$\frac{n+1}{2}•\frac{n-1}{2}$=$\frac{n+1}{2}$,
當n為偶數時,An的所有元素之和為2+4+6+…+n-(1+3+5+…+n-1)=$\frac{n+2}{2}•\frac{n}{2}$-$\frac{n}{2}•\frac{n}{2}$=$\frac{n}{2}$.
點評 本題主要考查數列通項、求和與不等式等知識,考查化歸與轉化的數學思想方法,以及抽象概括能力、運算求解能力和創新意識.


 出彩同步大試卷系列答案
出彩同步大試卷系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{\sqrt{15}}}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
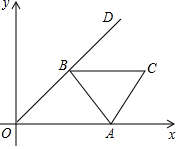 如圖,邊長為3的等邊三角形ABC的頂點A在x軸的正半軸上移動,∠AOD=30°,頂點B在射線,OD上隨之移動,則線段CO的最大值為3$\sqrt{3}$+3.
如圖,邊長為3的等邊三角形ABC的頂點A在x軸的正半軸上移動,∠AOD=30°,頂點B在射線,OD上隨之移動,則線段CO的最大值為3$\sqrt{3}$+3.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
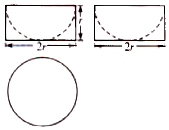 一個幾何體的三視圖如圖所示,其中俯視圖是半徑為r的圓,若該幾何體的體積為9π,則它的表面積是( )
一個幾何體的三視圖如圖所示,其中俯視圖是半徑為r的圓,若該幾何體的體積為9π,則它的表面積是( )| A. | 27π | B. | 36π | C. | 45π | D. | 54π |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
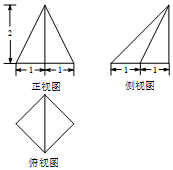
| A. | 2 | B. | $\sqrt{6}$ | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
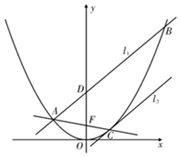 如圖,已知過拋物線E:x2=4y的焦點F的直線交拋物線E與A、C兩點,經過點A的直線l1分別交y軸、拋物線E于點D、B(B與C不重合),∠FAD=∠FDA,經過點C作拋物線E的切線為l2.
如圖,已知過拋物線E:x2=4y的焦點F的直線交拋物線E與A、C兩點,經過點A的直線l1分別交y軸、拋物線E于點D、B(B與C不重合),∠FAD=∠FDA,經過點C作拋物線E的切線為l2.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com