
分析 an+an-1=$\frac{n}{{a}_{n}-{a}_{n-1}}$+2(n≥2),取分母化為:$({a}_{n}-1)^{2}$-$({a}_{n-1}-1)^{2}$=n.利用“累加求和”可得$({a}_{n}-1)^{2}$,再利用“裂項求和”方法即可得出.
解答 解:∵an+an-1=$\frac{n}{{a}_{n}-{a}_{n-1}}$+2(n≥2),
∴${a}_{n}^{2}-{a}_{n-1}^{2}$=n+2(an-an-1),
化為:$({a}_{n}-1)^{2}$-$({a}_{n-1}-1)^{2}$=n.
∴$({a}_{n}-1)^{2}$=[$({a}_{n}-1)^{2}$-$({a}_{n-1}-1)^{2}$]+[$({a}_{n-1}-1)^{2}$-$({a}_{n-2}-1)^{2}]$+…+$[({a}_{2}-1)^{2}-({a}_{1}-1)^{2}]$+$({a}_{1}-1)^{2}$
=n+(n-1)+…+2+1=$\frac{n(n+1)}{2}$.
∴$\frac{1}{({a}_{n}-1)^{2}}$=$\frac{2}{n(n+1)}$=2$(\frac{1}{n}-\frac{1}{n+1})$.
∴$\frac{1}{({a}_{1}-1)^{2}}$+$\frac{1}{({a}_{2}-1)^{2}}$+…+$\frac{1}{({a}_{n}-1)^{2}}$=2$[(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n}-\frac{1}{n+1})]$
=2$(1-\frac{1}{n+1})$=$\frac{2n}{n+1}$.
故答案為:$\frac{2n}{n+1}$.
點評 本題考查了數列遞推關系、“累加求和”方法、“裂項求和”方法,考查了推理能力與計算能力,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | M∩N=M | B. | M∪(∁UN)=U | C. | M∩(∁UN)=∅ | D. | M⊆∁UN |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
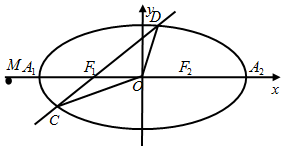 (文科)如圖,已知橢圓的中心在坐標原點,焦點F1,F2,在x軸上,長軸A1A2的長為4,x軸上一點M(${-\frac{a^2}{c},0}$),$|{\overrightarrow{M{A_1}}}|$=$2|{\overrightarrow{{A_1}{F_1}}}|$.
(文科)如圖,已知橢圓的中心在坐標原點,焦點F1,F2,在x軸上,長軸A1A2的長為4,x軸上一點M(${-\frac{a^2}{c},0}$),$|{\overrightarrow{M{A_1}}}|$=$2|{\overrightarrow{{A_1}{F_1}}}|$.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com