
分析 根據數列的遞推關系,構造數列{$\frac{1}{{x}_{n}}$},得到數列{$\frac{1}{{x}_{n}}$}是等差數列,結合等差數列的通項公式進行求解即可.
解答 解:∵$f(x)=\frac{4x}{x+4}{,_{\;}}且{x_1}=1,{x_{n+1}}=f({x_n})$,
∴xn+1=$\frac{4{x}_{n}}{{x}_{n}+4}$,
則$\frac{1}{{x}_{n+1}}$=$\frac{{x}_{n}+4}{4{x}_{n}}$=$\frac{1}{{x}_{n}}$+$\frac{1}{4}$,
即$\frac{1}{{x}_{n+1}}$-$\frac{1}{{x}_{n}}$=$\frac{1}{4}$,
則數列{$\frac{1}{{x}_{n}}$}是公差d=$\frac{1}{4}$的等差數列,首項為1,
則$\frac{1}{{x}_{n}}$=1+$\frac{1}{4}$(n-1),
則$\frac{1}{{x}_{2017}}$=1+$\frac{1}{4}×2016$=1+504=505,
則x2017=$\frac{1}{505}$,
故答案為:$\frac{1}{505}$
點評 本題主要考查遞推數列的應用,根據條件構造等差數列是解決本題的關鍵.綜合性較強,有一定的難度.


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:高中數學 來源: 題型:解答題
 如圖,在三棱錐P-ABC中,PA⊥底面ABC,∠BAC=90°.點D,E,N分別為棱PA,PC,BC的中點,M是線段AD的中點,PA=AC=4,AB=2.
如圖,在三棱錐P-ABC中,PA⊥底面ABC,∠BAC=90°.點D,E,N分別為棱PA,PC,BC的中點,M是線段AD的中點,PA=AC=4,AB=2.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 內心 | B. | 外心 | C. | 垂心 | D. | 重心 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 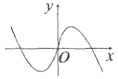 | B. | 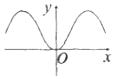 | C. | 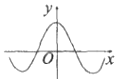 | D. | 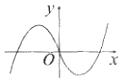 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
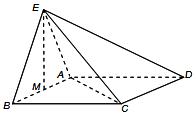 如圖,正三角形ABE與菱形ABCD所在的平面互相垂直,AB=2,∠ABC=60°,M是AB的中點.
如圖,正三角形ABE與菱形ABCD所在的平面互相垂直,AB=2,∠ABC=60°,M是AB的中點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com