
分析 (1)設乙班共有學生x名,則$\frac{8}{80}=\frac{6}{x}$,解得x=60.即乙班共有學生60名.由測試成績可知:A,B,C,E四名學生為優秀生,即可得出.
(2)至少有兩名優秀生的情況包括兩種:一種是只有兩名優秀學生,另一種是3名都是優秀生.利用互斥事件與相互獨立事件、古典概率計算公式即可得出.
(3)由已知可得:ξ的值為0,1,2,從乙班抽出的上述6名學生中隨機抽取1名是優秀生的概率為$\frac{2}{3}$.
則ξ~B$(2,\frac{2}{3})$,P(ξ=k)=${∁}_{2}^{k}(\frac{2}{3})^{k}(\frac{1}{3})^{2-k}$,即可得出分布列與數學期望.
解答 解:(1)設乙班共有學生x名,則$\frac{8}{80}=\frac{6}{x}$,解得x=60.即乙班共有學生60名.由測試成績可知:A,B,C,E四名學生為優秀生,∴$60×\frac{4}{6}$=40.
∴用上述樣本數據估計乙班優秀生的數量為40
(2)至少有兩名優秀生的情況包括兩種:一種是只有兩名優秀學生,另一種是3名都是優秀生.
∴要求的概率P=$\frac{{∁}_{4}^{2}{∁}_{2}^{1}+{∁}_{4}^{3}}{{∁}_{6}^{3}}$=$\frac{4}{5}$.
(3)由已知可得:ξ的值為0,1,2,從乙班抽出的上述6名學生中隨機抽取1名是優秀生的概率為$\frac{2}{3}$.
則ξ~B$(2,\frac{2}{3})$,P(ξ=k)=${∁}_{2}^{k}(\frac{2}{3})^{k}(\frac{1}{3})^{2-k}$,可得P(ξ=0)=$\frac{1}{9}$,P(ξ=1)=$\frac{4}{9}$,P(ξ=0)=$\frac{4}{9}$.
| ξ | 0 | 1 | 2 |
| P | $\frac{1}{9}$ | $\frac{4}{9}$ | $\frac{4}{9}$ |
點評 本題考查了分層抽樣、互斥事件與相互獨立事件、古典概率計算公式、二項分布列的計算公式與數學期望,考查了推理能力與計算能力,屬于中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | {1} | B. | ∅ | C. | [0,10] | D. | (0,10] |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 若向量$\overrightarrow{a}$∥$\overrightarrow{b}$,則存在唯一的實數λ,使得$\overrightarrow{a}$=λ$\overrightarrow{b}$ | |
| B. | 已知隨機變量ξ服從正態分布N(1,σ2),若P(ξ≤4)=0.79,則P(ξ≤-2)=0.21 | |
| C. | “φ=$\frac{3π}{2}$”是“y=sin(2x+φ)為偶函數”的充要條件 | |
| D. | 函數y=f(1+x)與函數y=f(1-x)的圖象關于直線x=1對稱 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
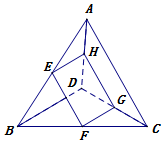 如圖,E,F,G,H分別是空間四邊形ABCD的邊AB,BC,CD,DA上的中點.
如圖,E,F,G,H分別是空間四邊形ABCD的邊AB,BC,CD,DA上的中點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com