
【題目】已知a∈R,命題p:“x∈[1,2],x2﹣a≥0”,命題q:“x∈R,x2+2ax+2﹣a=0”.
(1)若命題p為真命題,求實數a的取值范圍;
(2)若命題“p∨q”為真命題,命題“p∧q”為假命題,求實數a的取值范圍.
【答案】(1) (﹣∞,1] (2) a>1或﹣2<a<1
【解析】分析:第一問由于命題![]() ,令
,令![]() ,只要
,只要![]() 時,
時,![]() 即可;第二問由第一問可知,當命題
即可;第二問由第一問可知,當命題![]() 為真命題時,
為真命題時,![]() ,命題
,命題![]() 為真命題時,
為真命題時,![]() ,解得
,解得![]() 的取值范圍,由于命題“p∨q”為真命題,命題“p∧q”為假命題,可知命題p與命題q必然一真一假,解出即可.
的取值范圍,由于命題“p∨q”為真命題,命題“p∧q”為假命題,可知命題p與命題q必然一真一假,解出即可.
詳解:(1)∵命題p:“x∈[1,2],x2﹣a≥0”,令f(x)=x2﹣a,
根據題意,只要x∈[1,2]時,f(x)min≥0即可,
也就是1﹣a≥0,解得a≤1,
∴實數a的取值范圍是(﹣∞,1];
(2)由(1)可知,當命題p為真命題時,a≤1,
命題q為真命題時,△=4a2﹣4(2﹣a)≥0,解得a≤﹣2或a≥1.
∵命題“p∨q”為真命題,命題“p∧q”為假命題,
∴命題p與命題q必然一真一假,
當命題p為真,命題q為假時,![]() ,
,
當命題p為假,命題q為真時,![]() ,
,
綜上:a>1或﹣2<a<1.


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是直角梯形,側棱
是直角梯形,側棱![]() 底面
底面![]() 垂直于
垂直于![]() 和
和![]() ,
,![]()
![]() 是棱
是棱![]() 的中點.
的中點.
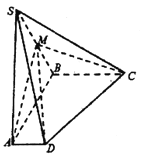
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的正弦值;
的正弦值;
(Ⅲ)在線段![]() 上是否存在一點
上是否存在一點![]() 使得
使得![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() 若存在,請求出
若存在,請求出![]() 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,直線
,直線![]() ,動圓P與圓M相外切,且與直線l相切.設動圓圓心P的軌跡為E.
,動圓P與圓M相外切,且與直線l相切.設動圓圓心P的軌跡為E.
(1)求E的方程;
(2)若點A,B是E上的兩個動點,O為坐標原點,且![]() ,求證:直線AB恒過定點.
,求證:直線AB恒過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,A(﹣2,0),B(2,0),P為不在x軸上的動點,直線PA,PB的斜率滿足kPAkPB![]() .
.
(1)求動點P的軌跡Γ的方程;
(2)若M,N是軌跡Γ上兩點,kMN=1,求△OMN面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左頂點為
的左頂點為![]() ,上頂點為
,上頂點為![]() ,右焦點為
,右焦點為![]() ,離心率為
,離心率為![]() ,
,![]() 的面積為
的面積為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)若![]() 為
為![]() 軸上的兩個動點,且
軸上的兩個動點,且![]() ,直線
,直線![]() 和
和![]() 分別與橢圓
分別與橢圓![]() 交于
交于![]() 兩點.
兩點.
(ⅰ)求![]() 的面積最小值;
的面積最小值;
(ⅱ)證明:![]() 三點共線.
三點共線.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某超市從2014年甲、乙兩種酸奶的日銷售量(單位:箱)的數據中分別隨機抽取100個,并按[ 0,10],(10,20],(20,30],(30,40],(40,50]分組,得到頻率分布直方圖如下:
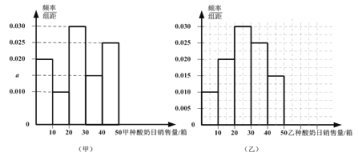
假設甲、乙兩種酸奶獨立銷售且日銷售量相互獨立.
(1)寫出頻率分布直方圖(甲)中的![]() 的值;記甲種酸奶與乙種酸奶日銷售量(單位:箱)的方差分別為
的值;記甲種酸奶與乙種酸奶日銷售量(單位:箱)的方差分別為![]() ,
,![]() ,試比較
,試比較![]() 與
與![]() 的大小;(只需寫出結論)
的大小;(只需寫出結論)
(2)估計在未來的某一天里,甲、乙兩種酸奶的銷售量恰有一個高于20箱且另一個不高于20箱的概率;
(3)設![]() 表示在未來3天內甲種酸奶的日銷售量不高于20箱的天數,以日銷售量落入各組的頻率作為概率,求
表示在未來3天內甲種酸奶的日銷售量不高于20箱的天數,以日銷售量落入各組的頻率作為概率,求![]() 的數學期望.
的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】銀川市展覽館22天中每天進館參觀的人數如下:
180 158 170 185 189 180 184 185 140 179 192
185 190 165 182 170 190 183 175 180 185 148
計算參觀人數的中位數、眾數、平均數、標準差(保留整數部分).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com