
【題目】已知函數(shù)![]() (
(![]() ).
).
(Ⅰ)若![]() 在點(diǎn)
在點(diǎn)![]() 處的切線與
處的切線與![]() 軸平行,且
軸平行,且![]() 在區(qū)間
在區(qū)間![]() 上存在最大值,求實(shí)數(shù)
上存在最大值,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(Ⅱ)當(dāng)![]() 時,求不等式
時,求不等式![]() 恒成立時
恒成立時![]() 的最小整數(shù)值.
的最小整數(shù)值.
【答案】(1)![]() (2)
(2)![]() 的最小整數(shù)值為
的最小整數(shù)值為![]() .
.
【解析】
試題(1)由導(dǎo)數(shù)幾何意義得![]() ,解得
,解得![]() .再根據(jù)
.再根據(jù)![]() 的正負(fù)討論導(dǎo)函數(shù)符號變化規(guī)律,確定單調(diào)性,進(jìn)而確定最值取法(2)根據(jù)變量分類法得
的正負(fù)討論導(dǎo)函數(shù)符號變化規(guī)律,確定單調(diào)性,進(jìn)而確定最值取法(2)根據(jù)變量分類法得![]() 最大值,利用導(dǎo)數(shù)研究函數(shù)
最大值,利用導(dǎo)數(shù)研究函數(shù)![]() 最大值
最大值![]() ,其中
,其中![]() ,因此化簡
,因此化簡![]() 得
得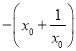 ,最后根據(jù)基本不等式求得最大值
,最后根據(jù)基本不等式求得最大值![]() ,再根據(jù)
,再根據(jù)![]() 得
得![]() 的最小整數(shù)值為
的最小整數(shù)值為![]() .
.
試題解析:解:(Ⅰ)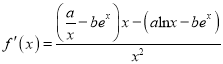
![]() .
.
∵![]() 在點(diǎn)
在點(diǎn)![]() 處的切線與
處的切線與![]() 軸平行,∴
軸平行,∴![]() ,∴
,∴![]() .
.
因此![]() ,
,
當(dāng)![]() 時,
時,![]() 在區(qū)間
在區(qū)間![]() 上為正,在區(qū)間
上為正,在區(qū)間![]() 上為負(fù),因此
上為負(fù),因此![]() 在區(qū)間
在區(qū)間![]() 上為增函數(shù),在區(qū)間
上為增函數(shù),在區(qū)間![]() 上為減函數(shù),即函數(shù)
上為減函數(shù),即函數(shù)![]() 在
在![]() 處取得唯一的極大值,即為最大值;
處取得唯一的極大值,即為最大值;
當(dāng)![]() 時,
時,![]() 在
在![]() 上為減函數(shù),在
上為減函數(shù),在![]() 為增函數(shù),即函數(shù)
為增函數(shù),即函數(shù)![]() 有最小值,無最大值.
有最小值,無最大值.
因此實(shí)數(shù)![]() 的取值范圍是
的取值范圍是![]() .
.
(Ⅱ)當(dāng)![]() 時,設(shè)
時,設(shè)![]() ,
,![]() 在區(qū)間
在區(qū)間![]() 上為減函數(shù),
上為減函數(shù),
又![]() ,
,![]() ,
,
因此存在唯一實(shí)數(shù)![]() ,使
,使![]() ,
,
由此得到![]() ,
,![]() ;
;
此時![]() 在區(qū)間
在區(qū)間![]() 上為增函數(shù),在區(qū)間
上為增函數(shù),在區(qū)間![]() 上為減函數(shù),
上為減函數(shù),
由單調(diào)性知![]()
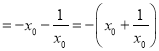 ,
,
又![]() ,故
,故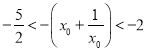 ,
,
因此![]() 恒成立時
恒成立時![]() ,即
,即![]() 的最小整數(shù)值為
的最小整數(shù)值為![]() .
.


 開心試卷期末沖刺100分系列答案
開心試卷期末沖刺100分系列答案 雙基同步導(dǎo)航訓(xùn)練系列答案
雙基同步導(dǎo)航訓(xùn)練系列答案 黃岡小狀元同步計(jì)算天天練系列答案
黃岡小狀元同步計(jì)算天天練系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知a∈R,命題p:“x∈[1,2],x2﹣a≥0”,命題q:“x∈R,x2+2ax+2﹣a=0”.
(1)若命題p為真命題,求實(shí)數(shù)a的取值范圍;
(2)若命題“p∨q”為真命題,命題“p∧q”為假命題,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)橢圓![]() 的左、右頂點(diǎn)分別為
的左、右頂點(diǎn)分別為![]() ,
,![]() ,且左、右焦點(diǎn)與短軸的一個端點(diǎn)是等邊三角形的三個頂點(diǎn),點(diǎn)
,且左、右焦點(diǎn)與短軸的一個端點(diǎn)是等邊三角形的三個頂點(diǎn),點(diǎn)![]() 在橢圓上,過點(diǎn)
在橢圓上,過點(diǎn)![]() 的直線交橢圓
的直線交橢圓![]() 于
于![]() 軸上方的點(diǎn)
軸上方的點(diǎn)![]() ,交直線
,交直線![]() 于點(diǎn)
于點(diǎn)![]() .直線
.直線![]() 與橢圓
與橢圓![]() 的另一交點(diǎn)為
的另一交點(diǎn)為![]() ,直線
,直線![]() 與直線
與直線![]() 交于點(diǎn)
交于點(diǎn)![]() .
.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)若![]() ,試求直線
,試求直線![]() 的方程;
的方程;
(3)如果![]() ,試求
,試求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,四邊形![]() 中(圖1),
中(圖1),![]() 是
是![]() 的中點(diǎn),
的中點(diǎn),![]() ,
,![]()
![]() ,
,![]() 將(圖1)沿直線
將(圖1)沿直線![]() 折起,使二面角
折起,使二面角![]() 為
為![]() (如圖2).
(如圖2).
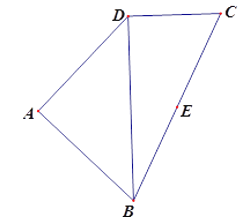
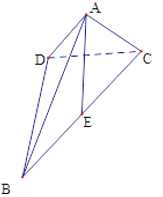
圖1 圖2
(1)求證:![]() 平面
平面![]() ;
;
(2)求異面直線![]() 與
與![]() 所成角的余弦值;
所成角的余弦值;
(3)求點(diǎn)![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】改革開放40年來,體育產(chǎn)業(yè)蓬勃發(fā)展反映了“健康中國”理念的普及.下圖是我國2006年至2016年體育產(chǎn)業(yè)年增加值及年增速圖.其中條形圖表示體育產(chǎn)業(yè)年增加值(單位:億元),折線圖為體育產(chǎn)業(yè)年增長率(%).
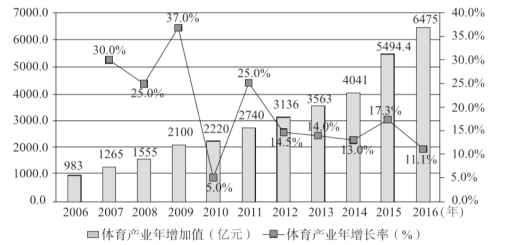
(Ⅰ)從2007年至2016年這十年中隨機(jī)選出一年,求該年體育產(chǎn)業(yè)年增加值比前一年多![]() 億元以上的概率;
億元以上的概率;
(Ⅱ)從2007年至2011年這五年中隨機(jī)選出兩年,求至少有一年體育產(chǎn)業(yè)年增長率超過25%的概率;
(Ⅲ)由圖判斷,從哪年開始連續(xù)三年的體育產(chǎn)業(yè)年增長率方差最大?從哪年開始連續(xù)三年的體育產(chǎn)業(yè)年增加值方差最大?(結(jié)論不要求證明)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,直線
中,直線![]() 的參數(shù)方程為:
的參數(shù)方程為:![]() (
(![]() 為參數(shù),
為參數(shù),![]() ),以
),以![]() 為極點(diǎn),
為極點(diǎn),![]() 軸的正半軸為極軸,建立極坐標(biāo)系,曲線
軸的正半軸為極軸,建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)當(dāng)![]() 時,寫出直線
時,寫出直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)若點(diǎn)![]() ,設(shè)曲線
,設(shè)曲線![]() 與直線
與直線![]() 交于點(diǎn)
交于點(diǎn)![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】將一顆骰子先后拋擲2次,觀察向上的點(diǎn)數(shù),求:
(1)兩數(shù)中至少有一個奇數(shù)的概率;
(2)以第一次向上的點(diǎn)數(shù)為橫坐標(biāo)x,第二次向上的點(diǎn)數(shù)為縱坐標(biāo)y的點(diǎn)(x,y)在圓x2+y2=15的外部或圓上的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 、
、![]() 分別是橢圓
分別是橢圓![]()
![]()
![]() 的左、右焦點(diǎn),點(diǎn)
的左、右焦點(diǎn),點(diǎn)![]() 是橢圓
是橢圓![]() 上一點(diǎn),且
上一點(diǎn),且![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() ,
,![]() 兩點(diǎn),若
兩點(diǎn),若![]() ,其中
,其中![]() 為坐標(biāo)原點(diǎn),判斷
為坐標(biāo)原點(diǎn),判斷![]() 到直線
到直線![]() 的距離是否為定值?若是,求出該定值;若不是,請說明理由.
的距離是否為定值?若是,求出該定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本小題滿分12分)貴廣高速鐵路自貴陽北站起,經(jīng)黔南州、黔東南、廣西桂林、賀州、廣東肇慶、佛山終至廣州南站. 其中廣東省內(nèi)有懷集站、廣寧站、肇慶東站、三水南站、佛山西站、廣州南站共6個站. 記者對廣東省內(nèi)的6個車站隨機(jī)抽取3個進(jìn)行車站服務(wù)滿意度調(diào)查.
(1)求抽取的車站中含有佛山市內(nèi)車站(包括三水南站和佛山西站)的概率;
(2)設(shè)抽取的車站中含有肇慶市內(nèi)車站(包括懷集站、廣寧站、肇慶東站)個數(shù)為X,求X的分布列及其均值(即數(shù)學(xué)期望).
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com