【題目】將一顆骰子先后拋擲2次，觀察向上的點數，求：
（1）兩數中至少有一個奇數的概率；
（2）以第一次向上的點數為橫坐標x，第二次向上的點數為縱坐標y的點（x，y）在圓x2+y2＝15的外部或圓上的概率.
【答案】（1）
；（2）
【解析】
（1）由題意，先算出向上的點（x，y）共有的基本事件的總數，再找出“兩數均為偶數”含有基本事件的個數，用古典概型求其概率，再用對立事件，求解“兩數中至少有一個奇數”事件的概率.
（2）先列舉出“點（x，y）在圓x2+y2＝15的內部”事件的基本事件的個數，求其概率，再利用對立事件，求 “點（x，y）在圓x2+y2＝15上或圓的外部”事件的概率
（1）由題意，先后拋擲2次，
向上的點（x，y）共有n＝6×6＝36種等可能結果，為古典概型.
記“兩數中至少有一個奇數”為事件B，
則事件B與“兩數均為偶數”為對立事件，記為
.
∵事件包含的基本事件數m＝3×3＝9.
∴P（）
，則P（B）＝1﹣P（）
，
因此，兩數中至少有一個奇數的概率為.
（2）點（x，y）在圓x2+y2＝15的內部記為事件C，
則
表示“點（x，y）在圓x2+y2＝15上或圓的外部”.
又事件C包含基本事件：
（1，1），（1，2），（1，3），（2，1），
（2，2），（2，3），（3，1），（3，2），共8種.
∴P（C）
，從而P（）＝1﹣P（C）＝1
.
∴點（x，y）在圓x2+y2＝15的外部或圓上的概率為.
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】某超市從2014年甲、乙兩種酸奶的日銷售量（單位：箱）的數據中分別隨機抽取100個，并按[ 0，10]，（10，20]，（20，30]，（30，40]，（40，50]分組，得到頻率分布直方圖如下：
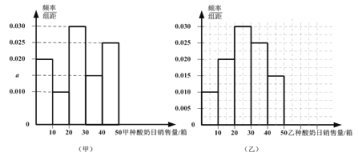
假設甲、乙兩種酸奶獨立銷售且日銷售量相互獨立．
（1）寫出頻率分布直方圖（甲）中的
的值；記甲種酸奶與乙種酸奶日銷售量（單位：箱）的方差分別為
，
，試比較與的大小；（只需寫出結論）
（2）估計在未來的某一天里，甲、乙兩種酸奶的銷售量恰有一個高于20箱且另一個不高于20箱的概率；
（3）設
表示在未來3天內甲種酸奶的日銷售量不高于20箱的天數，以日銷售量落入各組的頻率作為概率，求的數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
是定義在
上的奇函數，在
上是增函數，且
，給出下列結論，
①若
且
，則
；
②若
且
，則
；
③若方程
在
內恰有四個不同的實根
， 
， 
， 
，則
或8；
④函數
在
內至少有5個零點，至多有13個零點.
其中結論正確的有（ ）
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】定義在[﹣1，1]上的奇函數f（x）滿足當﹣1≤x＜0時，f（x）=
.
（1）求f（x）在[﹣1，1]上的解析式；
（2）當x∈（0，1]時，函數g（x）=
﹣m有零點，試求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列四個結論：
（1）若
，則
恒成立；
（2）命題“若
，則
”的逆否命題為“若
，則
”；
（3）“命題
為真”是“命題
為真”的充分不必要條件；
（4）命題“
”的否定是“
”．
其中正確的結論的個數是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知雙曲線
的焦點是橢圓
： 
（
）的頂點，且橢圓與雙曲線的離心率互為倒數.
（Ⅰ）求橢圓
的方程；
（Ⅱ）設動點
， 
在橢圓
上，且
，記直線
在
軸上的截距為
，求
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
