
分析 (Ⅰ)求出函數f(x)定義域為(0,+∞),f′(x)=lnx+1-a,由此利用導數性質能求出f(x)的單調區間及最小值.
(Ⅱ)令h(x)=f(x)-g(x),問題等價于hmin≥0,x∈[1,+∞),求出h′(x)=2ax+lnx-a-1,令m(x)=2ax+lnx-a-1,則${m}^{'}(x)=2a+\frac{1}{x}$,由此利用導數性質能求出a的取值范圍.
解答 解:(Ⅰ)∵f(x)=xlnx-ax,∴函數f(x)定義域為(0,+∞),…(1分)
f′(x)=lnx+1-a,令f′(x)>0,即lnx+1-a>0,得x>ea-1,
令f′(x)<0,即lnx+1-a<0,得0<x<ea-1,
∴f(x)的增區間為(ea-1,+∞),減區間為(0,ea-1),
∴fmin(x)=f(ea-1)=ea-1lnea-1-a•ea-1=-ea-1.…(4分)
(Ⅱ)∵f(x)≥g(x)在x∈[1,+∞)恒成立,令h(x)=f(x)-g(x),
∴問題等價于hmin≥0,x∈[1,+∞),…(5分)
∵h(x)=xlnx+ax2-ax-2x+2,
∴h′(x)=2ax+lnx-a-1,
令m(x)=2ax+lnx-a-1,則${m}^{'}(x)=2a+\frac{1}{x}$,
∵x≥1,a>0,∴${m}^{'}(x)=2a+\frac{1}{x}$>0,
∴m(x)在[1,+∞)上單調遞增,∴當x≥1時,m(x)≥m(1)=a-1,…(8分)
若m(1)=a-1≥0,即a≥1時,h′(x)=m(x)≥m(1)=a-1≥0恒成立,
此時h(x)=xlnx+ax2-ax-2x+2在x∈[1,+∞)上單調遞增,∴h(x)≥h(1)=0,
∴a≥1滿足題意…(11分)
下面證明當0<a<1不合題意,
當0<a<1時,∵h′(x)=2ax+lnx-a-1,h′(1)=a-1<0,h′(e)=2ae-a>0,
由上面可知h′(x)在[1,+∞)上單調遞增,
∴h′(x)=2ax+lnx-a-1=0在(1,e)上有唯一解,設為x0,
∴當x∈[1,x0)時,h′(x)<0,此時h(x0)<h(1)=0不合題意.
綜上a≥1.
∴a的取值范圍[1,+∞).
點評 本題考查函數的單調區間和最小值的求法,考查實數的取值范圍的求法,是中檔題,解題時要認真審題,注意構造法、等價轉化思想和導數性質的合理運用.


 口算能手系列答案
口算能手系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 3 | B. | 3+$\sqrt{2}$ | C. | 3-$\sqrt{2}$ | D. | 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 若α>β,則sinα>sinβ | |
| B. | 命題:“?x>1,x2>1”的否定是“?x≤1,x2≤1” | |
| C. | 直線ax+y+2=0與ax-y+4=0垂直的充要條件為a=±1 | |
| D. | “若xy=0,則x=0或y=0”的逆否命題為“若x≠0或y≠0,則xy≠0” |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
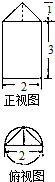 一個圓柱與一個三棱錐的組合體的正視圖和俯視圖如圖所示,則該幾何體的側視圖的面積為( )
一個圓柱與一個三棱錐的組合體的正視圖和俯視圖如圖所示,則該幾何體的側視圖的面積為( )| A. | 6 | B. | $\frac{13}{2}$ | C. | 7 | D. | 4π |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com