
���}Ŀ����֪![]() �ǒ��タ(xi��n)
�ǒ��タ(xi��n)![]() ��һ�c(di��n)����(j��ng)�^(gu��)�c(di��n)
��һ�c(di��n)����(j��ng)�^(gu��)�c(di��n)![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() �c���タ(xi��n)
�c���タ(xi��n)![]() ����
����![]() ��
��![]() ���c(di��n)����ͬ���c(di��n)
���c(di��n)����ͬ���c(di��n)![]() ����ֱ��(xi��n)
����ֱ��(xi��n)![]() ��
��![]() �քe��ֱ��(xi��n)
�քe��ֱ��(xi��n)![]() ���c(di��n)
���c(di��n)![]() ��
��![]() .
.
��1�����タ(xi��n)���̼��佹�c(di��n)����(bi��o)��
��2�����C����![]() ��ֱ���ĈAǡ�ý�(j��ng)�^(gu��)ԭ�c(di��n).
��ֱ���ĈAǡ�ý�(j��ng)�^(gu��)ԭ�c(di��n).
���𰸡���1�����タ(xi��n)���̞�![]() �����c(di��n)����(bi��o)��
�����c(di��n)����(bi��o)��![]() ����2���C��Ҋ(ji��n)����.
����2���C��Ҋ(ji��n)����.
��������
��1�����c(di��n)![]() ������(bi��o)���뒁�タ(xi��n)
������(bi��o)���뒁�タ(xi��n)![]() �ķ��̣����
�ķ��̣����![]() ��ֵ���ɵó����タ(xi��n)
��ֵ���ɵó����タ(xi��n)![]() �ķ��̣���������タ(xi��n)
�ķ��̣���������タ(xi��n)![]() �Ľ��c(di��n)����(bi��o)��
�Ľ��c(di��n)����(bi��o)��
��2���O(sh��)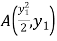 ��
��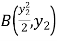 ��
��![]() ��
��![]() ���O(sh��)ֱ��(xi��n)
���O(sh��)ֱ��(xi��n)![]() �ķ��̞�
�ķ��̞�![]() ������
������![]() ����ֱ��(xi��n)
����ֱ��(xi��n)![]() �ķ����c���タ(xi��n)
�ķ����c���タ(xi��n)![]() �ķ���(li��n)�����г��f�_(d��)������������������(xi��n)����c(di��n)
�ķ���(li��n)�����г��f�_(d��)������������������(xi��n)����c(di��n)![]() ��
��![]() ������(bi��o)��Ȼ���f�_(d��)��������
������(bi��o)��Ȼ���f�_(d��)��������![]() ������������(sh��)���e������(bi��o)�\(y��n)��Ӌ(j��)���
������������(sh��)���e������(bi��o)�\(y��n)��Ӌ(j��)���![]() �������C�����Y(ji��)Փ����.
�������C�����Y(ji��)Փ����.
��1����![]() ����
����![]() ����
����![]() ����ˣ����タ(xi��n)���̞�
����ˣ����タ(xi��n)���̞�![]() �����c(di��n)����(bi��o)��
�����c(di��n)����(bi��o)��![]() ��
��
��2���O(sh��)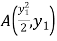 ��
��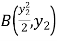 ��
��![]() ��
��![]() .
.
��?y��n)�ֱ��(xi��n)![]() ����(j��ng)�^(gu��)�c(di��n)
����(j��ng)�^(gu��)�c(di��n)![]() ������ֱ��(xi��n)
������ֱ��(xi��n)![]() һ����б�ʣ��O(sh��)ֱ��(xi��n)
һ����б�ʣ��O(sh��)ֱ��(xi��n)![]() ���̞�
���̞�![]() ��
��
�c���タ(xi��n)����(li��n)���õ�![]() ����ȥ
����ȥ![]() ����
����![]() ��
��
�t���f�_(d��)������![]() ��
��![]() .
.
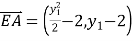 ��
��![]() ��
��
![]() ��
��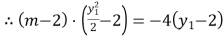 ����
����![]() ��
��
�@Ȼ��![]() ��
��![]() ��
��![]() ��
��
�t�c(di��n)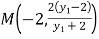 ��ͬ��������c(di��n)
��ͬ��������c(di��n)![]() ������(bi��o)��
������(bi��o)��![]() ��
��
���ԣ�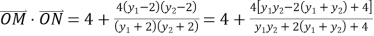
![]() ��
��
![]() ����ˣ���
����ˣ���![]() ��ֱ���ĈA�^(gu��)ԭ�c(di��n).
��ֱ���ĈA�^(gu��)ԭ�c(di��n).


 ��x��܇(ch��)ϵ�д�
��x��܇(ch��)ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��5G�W(w��ng)�j(lu��)�ǵ�����Ƅ�(d��ng)ͨ�žW(w��ng)�j(lu��)�����ֵ��Փ��ݔ�ٶȿ��_(d��)ÿ8��1GB����4G�W(w��ng)�j(lu��)�Ă�ݔ�ٶȿ씵(sh��)�ٱ����e����(l��i)�f(shu��)��һ��1G���Ӱ����8��֮��(n��i)���d��ɣ��S��5G���g(sh��)���Q���������ܽK�˷���3D�Ӱ���Α��Լ����߮�(hu��)�|(zh��)��UHD����(ji��)Ŀ�ĕr(sh��)�������҂��߁�(l��i)��ij�֙C(j��)�W(w��ng)�j(lu��)�аl(f��)��˾����һ��(g��)��(zhu��n)�I(y��)���g(sh��)�аl(f��)�F(tu��n)�(du��)��Q���N���g(sh��)��(w��n)�}�������Д�(sh��)�W(xu��)��(zhu��n)�I(y��)���I(y��)�����팣(zhu��n)�I(y��)���I(y��)��������(zhu��n)�I(y��)���I(y��)�ĸ��(l��i)�аl(f��)�ˆT��Ӌ(j��)1200�ˣ��F(xi��n)�ڹ�˾������аl(f��)ˮƽ�����÷ӳ�ӳ�ȡ400�˰���?j��n)?sh��)��(du��)�����ɿ�(j��)�M(j��n)�п��ˣ��������������l�ʷֲ�ֱ���D��ÿ�M���l��ҕ����ʣ���

��1���Ŀ��w��1200���W(xu��)�����S�C(j��)��ȡ1�ˣ���Ӌ(j��)���?j��n)?sh��)С��50�ĸ��ʣ�
��2���аl(f��)��˾�Q����(du��)�_(d��)��ij��?j��n)?sh��)���ϵ��аl(f��)�ˆT�M(j��n)�Ъ�(ji��ng)��(l��)��Ҫ��(ji��ng)��(l��)�аl(f��)�ˆT���˔�(sh��)�_(d��)��30%��Ո(q��ng)���Ӌ(j��)�@��(g��)��?j��n)?sh��)��ֵ��
��3����֪�ӱ���������֮���Ĕ�(sh��)�W(xu��)��(zhu��n)�I(y��)���I(y��)���аl(f��)�ˆT��?j��n)?sh��)������70�֣��ӱ��в�����70�ֵĔ�(sh��)�W(xu��)��(zhu��n)�I(y��)���I(y��)���аl(f��)�ˆT�˔�(sh��)�c������������(zhu��n)�I(y��)���I(y��)���аl(f��)�ˆT���˔�(sh��)����ȣ���Ӌ(j��)���w�Д�(sh��)�W(xu��)��(zhu��n)�I(y��)���I(y��)���аl(f��)�ˆT���˔�(sh��)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��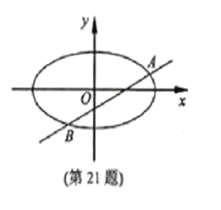
�����}�M(m��n)��15�֣���֪m��1��ֱ��(xi��n)![]() ��
��
�E�A![]() ��
��![]() �քe��E�A
�քe��E�A![]() �����ҽ��c(di��n).
�����ҽ��c(di��n).
��������(d��ng)ֱ��(xi��n)![]() �^(gu��)�ҽ��c(di��n)
�^(gu��)�ҽ��c(di��n)![]() �r(sh��)����ֱ��(xi��n)
�r(sh��)����ֱ��(xi��n)![]() �ķ��̣�
�ķ��̣�
�������O(sh��)ֱ��(xi��n)![]() �c�E�A
�c�E�A![]() ����
����![]() ���c(di��n)��
���c(di��n)��![]() ��
��
![]() �����ķքe��
�����ķքe��![]() .��ԭ�c(di��n)
.��ԭ�c(di��n)![]() ���Ծ�(xi��n)��
���Ծ�(xi��n)��
![]() ��ֱ���ĈA��(n��i)����(sh��)��(sh��)
��ֱ���ĈA��(n��i)����(sh��)��(sh��)![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D���c(di��n)![]() ��A
��A![]() ��
��![]() ��һ��(d��ng)�c(di��n)���^(gu��)�c(di��n)
��һ��(d��ng)�c(di��n)���^(gu��)�c(di��n)![]() �քe��
�քe��![]() �S��
�S��![]() �S�Ĵ���(xi��n)������քe��
�S�Ĵ���(xi��n)������քe��![]() ��
��![]() ���B��
���B��![]() ���L(zh��ng)���c(di��n)
���L(zh��ng)���c(di��n)![]() ��ʹ��
��ʹ��![]() ���c(di��n)
���c(di��n)![]() ��܉�Eӛ������(xi��n)
��܉�Eӛ������(xi��n)![]() .
.
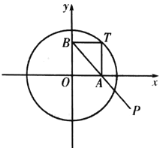
��1��������(xi��n)![]() �ķ��̣�
�ķ��̣�
��2�����c(di��n)![]() ��
��![]() �քeλ��
�քeλ��![]() �S�c
�S�c![]() �S�������S�ϣ�ֱ��(xi��n)
�S�������S�ϣ�ֱ��(xi��n)![]() �c����(xi��n)
�c����(xi��n)![]() �ཻ��
�ཻ��![]() ��
��![]() ���c(di��n)��ԇ��(w��n)������(xi��n)
���c(di��n)��ԇ��(w��n)������(xi��n)![]() ���Ƿ�����c(di��n)
���Ƿ�����c(di��n)![]() ��ʹ����߅��
��ʹ����߅��![]() ��ƽ����߅�Σ������ڣ����ֱ��(xi��n)
��ƽ����߅�Σ������ڣ����ֱ��(xi��n)![]() ���̣��������ڣ��f(shu��)������.
���̣��������ڣ��f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵ![]() �У���(d��ng)�A
����(d��ng)�A![]() �c�A
�c�A![]() �����c�A
�����c�A![]() ��(n��i)��
��(n��i)��
��1�����(d��ng)�A�A��![]() ��܉�E���̣�
��܉�E���̣�
��2��ֱ��(xi��n)![]() �^(gu��)�c(di��n)
�^(gu��)�c(di��n)![]() ���c��(d��ng)�A�A��
���c��(d��ng)�A�A��![]() ��܉�E����
��܉�E����![]() ��
��![]() ���c(di��n)���Ƿ����
���c(di��n)���Ƿ����![]() ��e�����ֵ�������ڣ����
��e�����ֵ�������ڣ����![]() ����e���������ڣ��f(shu��)������.
����e���������ڣ��f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���O(sh��)����(xi��n)![]() �����ɵķ��]�^(q��)��?y��n)?/span>D.
�����ɵķ��]�^(q��)��?y��n)?/span>D.
��1����^(q��)��D����e��
��2���O(sh��)�^(gu��)�c(di��n)![]() ��ֱ��(xi��n)�c����(xi��n)C���ڃ��c(di��n)P��Q����
��ֱ��(xi��n)�c����(xi��n)C���ڃ��c(di��n)P��Q����![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����![]() �У�
�У�![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ��
��![]() �ϵ��c(di��n)��
�ϵ��c(di��n)��![]()
![]() ��
��![]() �����c(di��n)����
�����c(di��n)����![]() ������
������![]() ����ʹƽ��
����ʹƽ��![]() ƽ��
ƽ��![]() .
.
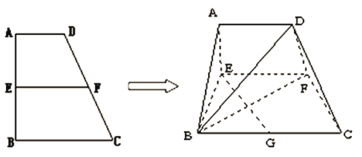
��1����(d��ng)![]() �r(sh��)�����C��
�r(sh��)�����C��![]() ��
��
��2��ӛ��![]() ����c(di��n)�������F���w�e��
����c(di��n)�������F���w�e��![]() ����
����![]() �����ֵ��
�����ֵ��
��3����(d��ng)![]() ȡ�����ֵ�r(sh��)��������
ȡ�����ֵ�r(sh��)��������![]() �Ĵ�С.
�Ĵ�С.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�������f(shu��)�������_���ǣ� ��
A. ��![]() ���ǡ�
���ǡ�![]() �������ij�ֲ���Ҫ�l��
�������ij�ֲ���Ҫ�l��
B. ���}![]() ���t
���t![]()
C. �����˽�800���W(xu��)����(du��)�W(xu��)Уij�(xi��ng)�̸�ԇ�(y��n)����Ҋ(ji��n)����ϵ�y(t��ng)��ӵķ������г�ȡһ��(g��)������40�Ęӱ����t�ֽM�ĽM����40
D. ��֪�ؚwֱ��(xi��n)��б�ʵĹ�Ӌ(j��)ֵ��1.23���ӱ��c(di��n)�����Ğ�![]() ���t�ؚwֱ��(xi��n)���̞�
���t�ؚwֱ��(xi��n)���̞�![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
��1��������(sh��)![]() ��
��![]() ����2��(g��)���c(di��n)����(sh��)��(sh��)
����2��(g��)���c(di��n)����(sh��)��(sh��)![]() ��ȡֵ����.��ע
��ȡֵ����.��ע![]() ��
��
��2���O(sh��)![]() ��������(sh��)
��������(sh��)![]() ǡ�Ѓɂ�(g��)��ͬ�ĘOֵ�c(di��n)
ǡ�Ѓɂ�(g��)��ͬ�ĘOֵ�c(di��n)![]() ��
��![]() ���C����
���C����![]() .
.
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com