
分析 (1)直線MN的方程為:$\frac{x}{a}$+$\frac{y}{-1}$=1,即x-ay-a=0.由$\frac{a}{\sqrt{1+{a}^{2}}}$=$\frac{\sqrt{3}}{2}$,解得a=$\sqrt{3}$.利用$c=\sqrt{{a}^{2}-{b}^{2}}$,即可的得出.H的離心率e=$\frac{c}{a}$.
(2)由(1)可知:橢圓H的標準方程為:$\frac{{x}^{2}}{3}+{y}^{2}$=1,設A(x1,y1),B(x2,y2).由$\overrightarrow{OC}$=$\frac{1}{2}\overrightarrow{OA}$+$\frac{\sqrt{3}}{2}$$\overrightarrow{OB}$,可得C$(\frac{1}{2}{x}_{1}+\frac{\sqrt{3}}{2}{x}_{2},\frac{1}{2}{y}_{1}+\frac{\sqrt{3}}{2}{y}_{2})$,利用A,B,C都在橢圓上整理化簡可得:x1x2+3y1y2=0.設直線l的方程為:x=my+$\sqrt{2}$,代入橢圓方程可得:(m2+3)y2+2$\sqrt{2}$my-1=0,利用根與系數的關系代入可得m,對直線l的斜率為0時,直接驗證即可.
解答 解:(1)直線MN的方程為:$\frac{x}{a}$+$\frac{y}{-1}$=1,即x-ay-a=0.∵$\frac{a}{\sqrt{1+{a}^{2}}}$=$\frac{\sqrt{3}}{2}$,解得a=$\sqrt{3}$.
又b=1,則$c=\sqrt{{a}^{2}-{b}^{2}}$=$\sqrt{2}$.
∴該橢圓H的離心率e=$\frac{c}{a}$=$\frac{\sqrt{2}}{\sqrt{3}}$=$\frac{\sqrt{6}}{3}$.
(2)由(1)可知:橢圓H的標準方程為:$\frac{{x}^{2}}{3}+{y}^{2}$=1,設A(x1,y1),B(x2,y2).
∵$\overrightarrow{OC}$=$\frac{1}{2}\overrightarrow{OA}$+$\frac{\sqrt{3}}{2}$$\overrightarrow{OB}$,∴C$(\frac{1}{2}{x}_{1}+\frac{\sqrt{3}}{2}{x}_{2},\frac{1}{2}{y}_{1}+\frac{\sqrt{3}}{2}{y}_{2})$,由A,B,C都在橢圓上,∴${x}_{1}^{2}+3{y}_{1}^{2}$=3,①${x}_{2}^{2}+3{y}_{2}^{2}$=3,②$(\frac{1}{2}{x}_{1}+\frac{\sqrt{3}}{2}{x}_{2})^{2}$+3$(\frac{1}{2}{y}_{1}+\frac{\sqrt{3}}{2}{y}_{2})^{2}$=3,③,由③化簡整理可得:$\frac{1}{4}$(${x}_{1}^{2}+3{y}_{1}^{2}$)+$\frac{3}{4}$(${x}_{2}^{2}+3{y}_{2}^{2}$)+$\frac{\sqrt{3}}{2}$(x1x2+3y1y2)=3,
把①②代入化簡可得:x1x2+3y1y2=0,④.設直線l的方程為:x=my+$\sqrt{2}$,代入橢圓方程可得:(m2+3)y2+2$\sqrt{2}$my-1=0,∴y1+y2=$\frac{-2\sqrt{2}m}{{m}^{2}+3}$,y1•y2=$\frac{-1}{{m}^{2}}$+3,
∴x1x2=$(m{y}_{1}+\sqrt{2})$$(m{y}_{2}+\sqrt{2})$=m2y1y2+$\sqrt{2}$m(y1+y2)+2,
∴(m2+3)y1•y2+$\sqrt{2}$m(y1+y2)+2=0,
∴(m2+3)•$\frac{-1}{{m}^{2}}$+$\sqrt{2}$m•$\frac{-2\sqrt{2}m}{{m}^{2}+3}$+2=0,解得m=±1.
∴直線l的方程為x=±y+$\sqrt{2}$.
當直線l的斜率為0時,其方程為:y=0,此時A($\sqrt{3}$,0),B(-$\sqrt{3}$,0),不滿足④,舍去.
綜上可得:直線l的方程為x=±y+$\sqrt{2}$.
點評 本題考查了橢圓的標準方程及其性質、向量坐標運算性質、一元二次方程的根與系數的關系,考查了分類討論方法、推理能力與計算能力,屬于難題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 級 數 | 全月應納稅所得額 | 稅 率 |
| 1 | 不超過 1500元的部分 | 5% |
| 2 | 超過 1500元至4500元的部分 | 10% |
| 3 | 超過 4500元至9000元的部分 | 20% |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,四棱錐P-ABCD中,底面ABCD為矩形,PA⊥平面ABCD,AP=1,AD=$\sqrt{3}$,E為線段PD上一點,記$\frac{PE}{PD}$=λ. 當λ=$\frac{1}{2}$時,二面角D-AE-C的平面角的余弦值為$\frac{2}{3}$.
如圖,四棱錐P-ABCD中,底面ABCD為矩形,PA⊥平面ABCD,AP=1,AD=$\sqrt{3}$,E為線段PD上一點,記$\frac{PE}{PD}$=λ. 當λ=$\frac{1}{2}$時,二面角D-AE-C的平面角的余弦值為$\frac{2}{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
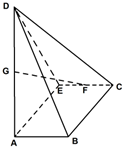 已知底面為矩形的四棱錐D-ABCE,AB=1,BC=2,AD=3,DE=$\sqrt{5}$,DE⊥AE,G、F分別為AD,CE的中點,其中二面角D-AE-C的平面角的正切值為-tan2.
已知底面為矩形的四棱錐D-ABCE,AB=1,BC=2,AD=3,DE=$\sqrt{5}$,DE⊥AE,G、F分別為AD,CE的中點,其中二面角D-AE-C的平面角的正切值為-tan2.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com