
分析 (1)化f(x)為sinx的二次函數,設sinx=t,則函數g(t)是開口向下,
對稱軸為t=$\frac{a}{2}$的拋物線,根據二次函數的性質,對a討論求出函數最大值;
(2)由M(a)=2求出對應的a值即可.
解答 解:(1)f(x)=cos2x+asinx-$\frac{a}{4}$-$\frac{1}{2}$
=(1-sin2x)+asinx-$\frac{a}{4}$-$\frac{1}{2}$
=-sin2x+asinx+$\frac{2-a}{4}$,
∵0≤x≤$\frac{π}{2}$,∴0≤sinx≤1;
設sinx=t,則
g(t)=-t2+at+$\frac{2-a}{4}$,t∈[0,1];
∴f(x)的最大值為
M(a)=$\left\{\begin{array}{l}{\frac{3}{4}a-\frac{1}{2},a≥2}\\{{\frac{1}{4}a}^{2}-\frac{1}{4}a+\frac{1}{2},0<a<2}\end{array}\right.$;
(2)當M(a)=2時,
若a≥2,則$\frac{3}{4}$a-$\frac{1}{2}$=2,解得a=$\frac{10}{3}$;
若0<a<2,則$\frac{1}{4}$a2-$\frac{1}{4}$a+$\frac{1}{2}$=2,
解得a=-2或a=3,不合題意,舍去;
綜上,a的值是$\frac{10}{3}$.
點評 本題主要考查了三角函數恒等變換的應用和二次函數的性質問題,是中檔題.


 步步高達標卷系列答案
步步高達標卷系列答案科目:高中數學 來源: 題型:解答題
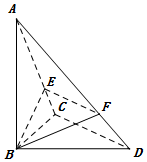 在三棱錐A-BCD中,AB⊥平面BCD,∠BCD=90°,E、F分別是AC、AD上的點,且$\frac{AE}{AC}=\frac{AF}{AD}$.
在三棱錐A-BCD中,AB⊥平面BCD,∠BCD=90°,E、F分別是AC、AD上的點,且$\frac{AE}{AC}=\frac{AF}{AD}$.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (1,-2) | B. | (-1,2) | C. | (-2,1) | D. | (2,-1) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,3) | B. | [0,4] | C. | [3,4) | D. | (-1,3) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 48種 | B. | 72種 | C. | 96種 | D. | 108種 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com