
分析 根據題意知X的所有可能取值,計算對應的概率值,寫出隨機變量X的分布列,再計算數學期望值.
解答 解:根據題意,X的所有可能取值0、1、2、3,
則$P(x=0)=C_2^0{(\frac{2}{5})^0}{(\frac{3}{5})^2}\frac{1}{5}=\frac{9}{125}$,
$P(x=1)=C_2^1{(\frac{2}{5})^1}{(\frac{3}{5})^1}\frac{1}{5}+C_2^0{(\frac{2}{5})^0}{(\frac{3}{5})^2}\frac{4}{5}=\frac{48}{125}$,
$P(x=2)=C_2^2{(\frac{2}{5})^2}{(\frac{3}{5})^0}\frac{1}{5}+C_2^1{(\frac{2}{5})^1}{(\frac{3}{5})^1}\frac{4}{5}=\frac{52}{125}$,
$P(x=3)=C_2^2{(\frac{2}{5})^2}{(\frac{3}{5})^0}\frac{4}{5}=\frac{16}{125}$;
所以隨機變量X的分布列為:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{9}{125}$ | $\frac{48}{125}$ | $\frac{52}{125}$ | $\frac{16}{125}$ |
點評 本題考查了離散型隨機變量的分布列與數學期望的計算問題,是基礎題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{7}{15}$ | B. | $\frac{3}{5}$ | C. | $\frac{11}{15}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
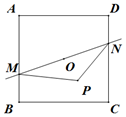 正方形ABCD邊長為2,中心為O,直線l經過中心O,交AB于M,交CD于N,P為平面上一點,且$2\overrightarrow{OP}=λ\overrightarrow{OB}+(1-λ)\overrightarrow{OC}$,則$\overrightarrow{PM}•\overrightarrow{PN}$的最小值是( )
正方形ABCD邊長為2,中心為O,直線l經過中心O,交AB于M,交CD于N,P為平面上一點,且$2\overrightarrow{OP}=λ\overrightarrow{OB}+(1-λ)\overrightarrow{OC}$,則$\overrightarrow{PM}•\overrightarrow{PN}$的最小值是( )| A. | $-\frac{3}{4}$ | B. | -1 | C. | $-\frac{7}{4}$ | D. | -2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com