
| A. | 4 | B. | 4 | C. | 12 | D. | 16 |
分析 ∵a>0,b>0,∴不等式$\frac{mab}{3a+b}≤a+3b$恒成立⇒m≤$\frac{(3a+b)(a+3b)}{ab}=\frac{10ab+3{a}^{2}+3{b}^{2}}{ab}$=10+$\frac{3{a}^{2}+3{b}^{2}}{ab}$,求出=10+$\frac{3{a}^{2}+3{b}^{2}}{ab}$的最小值即可.
解答 解:∵a>0,b>0,∴不等式$\frac{mab}{3a+b}≤a+3b$恒成立⇒m≤$\frac{(3a+b)(a+3b)}{ab}=\frac{10ab+3{a}^{2}+3{b}^{2}}{ab}$=10+$\frac{3{a}^{2}+3{b}^{2}}{ab}$,∵10+$\frac{3{a}^{2}+3{b}^{2}}{ab}≥10+\frac{2\sqrt{9{a}^{2}{b}^{2}}}{ab}=16$,∴m≤16,故選:D
點評 本題主要考查基本不等式的應用,函數的恒成立問題,屬于基礎題.


科目:高中數學 來源: 題型:選擇題
| A. | f(x)=4x3+x | B. | $f(x)=ln\frac{5-x}{5+x}$ | C. | $f(x)=tan\frac{x}{2}$ | D. | f(x)=ex+e-x |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 3 | B. | $\frac{7}{2}$ | C. | 4 | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\left\{\begin{array}{l}{a=-1}\\{b=0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=1}\\{b=0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=0}\\{b=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=0}\\{b=-1}\end{array}\right.$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題

| A. | (-∞,-2)∪(1,+∞) | B. | (-∞,-2)∪(1,2) | C. | (-∞,-1)∪(-1,1)∪(3,+∞) | D. | (-∞,-1)∪(-1,0)∪(2,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
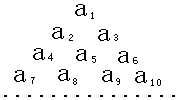 已知數列{an}是首項為1,公差為2的等差數列,將數列{an}中的各項排成如圖所示的一個三角形數表,記A(i,j)表示第i行從左至右的第j個數,例如A(4,3)=a9,則A(10,2)=93.
已知數列{an}是首項為1,公差為2的等差數列,將數列{an}中的各項排成如圖所示的一個三角形數表,記A(i,j)表示第i行從左至右的第j個數,例如A(4,3)=a9,則A(10,2)=93.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 72.705尺 | B. | 61.395尺 | C. | 61.905尺 | D. | 73.995尺 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com