
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 根據向量加法的平行四邊形法則,知O是BC的中點,由△ABC的外接圓的圓心為O,知BC是圓O的直徑,從而求得AB⊥AC,另由|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|,可得∠ABC=60°,故利用向量數量積的定義可以求得
解答 解:∵△ABC的外接圓的圓心為O,半徑為1,2$\overrightarrow{AO}$=$\overrightarrow{AB}$+$\overrightarrow{AC}$,
∴O是BC的中點,且BC是圓O的直徑,
∴AB⊥AC,AO=1,BC=2,
∵|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|,
∴AB=1,∴∠ABC=60°,
∴$\overrightarrow{BA}$•$\overrightarrow{BC}$=1×2×cos60°=1,
故選A.
點評 此題是個基礎題.考查向量在幾何中的應用,以及直角三角形有關的性質,同時考查學生靈活應用知識分析解決問題的能力和計算能力.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{5π}{4}$ | B. | -$\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | -$\frac{3}{4}$π |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-1,+∞) | B. | (-1,1) | C. | (-∞,1) | D. | [-1,1] |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
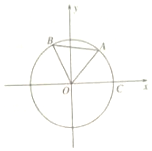 如圖,點A,B是單位圓O上的兩點,A,B點分別在第一,而象限,點C是圓O與x軸正半軸的交點,若∠COA=60°,∠AOB=α,點B的坐標為(-$\frac{3}{5}$,$\frac{4}{5}$).
如圖,點A,B是單位圓O上的兩點,A,B點分別在第一,而象限,點C是圓O與x軸正半軸的交點,若∠COA=60°,∠AOB=α,點B的坐標為(-$\frac{3}{5}$,$\frac{4}{5}$).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com