
分析 由導(dǎo)數(shù)的幾何意義,求得切線方程,聯(lián)立求得P點(diǎn)坐標(biāo),設(shè)直線MN的方程,代入拋物線方程,利用韋達(dá)定理求得x0=k,y0=-b,代入直線方程,即可求得直線MN方程,即可求得直線恒過(guò)定點(diǎn).
解答 解:設(shè)M(x1,$\frac{1}{2}$x12),B(x2,$\frac{1}{2}$x22),P(x0,y0).
∵y=$\frac{1}{2}$x2,∴y′=x.
則在點(diǎn)M處的切線方程為y-$\frac{1}{2}$x12=x1(x-x1),化為y=x1x-$\frac{1}{2}$x12.①
同理在點(diǎn)B處的切線方程為y=x2x-$\frac{1}{2}$x22.②
由①②得2x0=x1+x2,2y0=x1x2,顯然直線AB存在斜率.
設(shè)直線MN的方程是y=kx+b,
$\left\{\begin{array}{l}{y=kx+b}\\{y=\frac{1}{2}{x}^{2}}\end{array}\right.$,得x2-2kx-2b=0,
∴x1+x2=2k,x1x2=-2b,即x0=k,y0=-b,
代入x0-y0-2=0,得b=2-k,
∴y=kx+b=kx+2-k,
∴y-2=k(x-1)
因此直線MN恒過(guò)定點(diǎn)(1,2),
故答案為:(1,2).
點(diǎn)評(píng) 本題考查導(dǎo)數(shù)的幾何意義,利用導(dǎo)數(shù)求函數(shù)的切線方程,直線與拋物線的位置關(guān)系,考查計(jì)算能力,屬于中檔題.


 互動(dòng)課堂系列答案
互動(dòng)課堂系列答案 激活思維智能訓(xùn)練課時(shí)導(dǎo)學(xué)練系列答案
激活思維智能訓(xùn)練課時(shí)導(dǎo)學(xué)練系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | (-1,2) | B. | (0,1) | C. | (-1,0) | D. | (1,2) |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
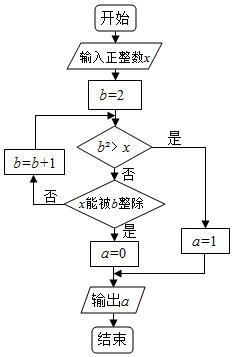 執(zhí)行兩次如圖所示的程序框圖,若第一次輸入的x值為7,第二次輸入的x值為9,則第一次,第二次輸出的a值分別為( )
執(zhí)行兩次如圖所示的程序框圖,若第一次輸入的x值為7,第二次輸入的x值為9,則第一次,第二次輸出的a值分別為( )| A. | 0,0 | B. | 1,1 | C. | 0,1 | D. | 1,0 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | [-2,2] | B. | $[-2\sqrt{3},2]$ | C. | $[-2,2\sqrt{3}]$ | D. | $[-2\sqrt{3},2\sqrt{3}]$ |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com