
分析 由已知,數列{an}為單調遞增數列,得出an+1-an>0對于任意n∈N*都成立,即有2n+1+λ>0,采用分離參數法求實數λ的取值范圍即可.
解答 解:∵an=n2+λn①
∴an+1=(n+1)2+λ(n+1)②
②-①得an+1-an=2n+1+λ.
由已知,數列{an}為單調遞增數列,
則an+1-an>0對于任意n∈N*都成立,即 2n+1+λ>0.
移向得λ>-(2n+1),λ只需大于-(2n+1)的最大值即可,
易知當n=1時,-(2n+1)的最大值 為-3,
∴λ>-3
故答案為:(-3,+∞).
點評 本題考查數列的函數性質,考查了轉化、計算能力,分離參數法的應用,屬于中檔題.


 高中必刷題系列答案
高中必刷題系列答案科目:高中數學 來源: 題型:選擇題
| A. | {0,1} | B. | {0,1,2} | C. | {1,2} | D. | {-1,0,1} |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (2,+∞) | B. | $(-∞,\frac{1}{2})$ | C. | $(\frac{1}{2},2)$ | D. | $(0,\frac{1}{2})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
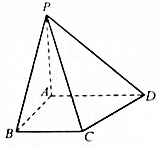 在四棱錐P-ABCD中,四邊形ABCD是梯形,AD∥BC
在四棱錐P-ABCD中,四邊形ABCD是梯形,AD∥BC查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com