
【題目】已知拋物線![]() 的焦點曲線
的焦點曲線![]() 的一個焦點,
的一個焦點, ![]() 為坐標原點,點
為坐標原點,點![]() 為拋物線
為拋物線![]() 上任意一點,過點
上任意一點,過點![]() 作
作![]() 軸的平行線交拋物線的準線于
軸的平行線交拋物線的準線于![]() ,直線
,直線![]() 交拋物線于點
交拋物線于點![]() .
.
(Ⅰ)求拋物線![]() 的方程;
的方程;
(Ⅱ)求證:直線![]() 過定點
過定點![]() ,并求出此定點的坐標.
,并求出此定點的坐標.
【答案】(I)![]() ;(II)證明見解析.
;(II)證明見解析.
【解析】試題分析:(Ⅰ)將曲線![]() 化為標準方程,可求得
化為標準方程,可求得![]() 的焦點坐標分別為
的焦點坐標分別為![]() ,可得
,可得![]() ,所以
,所以![]() ,即拋物線的方程為
,即拋物線的方程為![]() ;(Ⅱ)結合(Ⅰ),可設
;(Ⅱ)結合(Ⅰ),可設![]() ,得
,得 ,從而直線
,從而直線![]() 的方程為
的方程為![]() ,聯立直線與拋物線方程得
,聯立直線與拋物線方程得![]() ,解得
,解得![]() ,直線
,直線![]() 的方程為
的方程為 ,整理得
,整理得![]() 的方程為
的方程為![]() ,此時直線恒過定點
,此時直線恒過定點![]() .
.
試題解析:(Ⅰ)由曲線![]() ,化為標準方程可得
,化為標準方程可得 , 所以曲線
, 所以曲線 是焦點在
是焦點在![]() 軸上的雙曲線,其中
軸上的雙曲線,其中![]() ,故
,故![]() ,
, ![]() 的焦點坐標分別為
的焦點坐標分別為![]() ,因為拋物線的焦點坐標為
,因為拋物線的焦點坐標為![]() ,由題意知
,由題意知![]() ,所以
,所以![]() ,即拋物線的方程為
,即拋物線的方程為![]() .
.
(Ⅱ)由(Ⅰ)知拋物線![]() 的準線方程為
的準線方程為![]() ,設
,設![]() ,顯然
,顯然![]() .故
.故 ,從而直線
,從而直線![]() 的方程為
的方程為![]() ,聯立直線與拋物線方程得
,聯立直線與拋物線方程得![]() ,解得
,解得![]()
①當![]() ,即
,即![]() 時,直線
時,直線![]() 的方程為
的方程為![]() ,
,
②當![]() ,即
,即![]() 時,直線
時,直線![]() 的方程為
的方程為 ,整理得
,整理得![]() 的方程為
的方程為![]() ,此時直線恒過定點
,此時直線恒過定點![]() ,
, ![]() 也在直線
也在直線![]() 的方程為
的方程為![]() 上,故直線
上,故直線![]() 的方程恒過定點
的方程恒過定點![]() .
.
【題型】解答題
【結束】
21
【題目】已知函數![]() ,
, ![]()
(Ⅰ)當![]() 時,求函數
時,求函數![]() 的單調遞減區間;
的單調遞減區間;
(Ⅱ)若![]() 時,關于
時,關于![]() 的不等式
的不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(Ⅲ)若數列![]() 滿足
滿足![]() ,
, ![]() ,記
,記![]() 的前
的前![]() 項和為
項和為![]() ,求證:
,求證: ![]() .
.
【答案】(I)![]() ;(II)
;(II)![]() ;(III)證明見解析.
;(III)證明見解析.
【解析】試題分析:(Ⅰ)求出![]() ,在定義域內,分別令
,在定義域內,分別令![]() 求得
求得![]() 的范圍,可得函數
的范圍,可得函數![]() 增區間,
增區間, ![]() 求得
求得![]() 的范圍,可得函數
的范圍,可得函數![]() 的減區間;(Ⅱ)當
的減區間;(Ⅱ)當![]() 時,因為
時,因為![]() ,所以
,所以![]() 顯然不成立,先證明因此
顯然不成立,先證明因此![]() 時,
時, ![]() 在
在![]() 上恒成立,再證明當
上恒成立,再證明當![]() 時不滿足題意,從而可得結果;(III)先求出等差數列的前
時不滿足題意,從而可得結果;(III)先求出等差數列的前![]() 項和為
項和為![]() ,結合(II)可得
,結合(II)可得![]() ,各式相加即可得結論.
,各式相加即可得結論.
試題解析:(Ⅰ)由![]() ,得
,得![]() .所以
.所以![]()
令![]() ,解得
,解得![]() 或
或![]() (舍去),所以函數
(舍去),所以函數![]() 的單調遞減區間為
的單調遞減區間為 ![]() .
.
(Ⅱ)由![]() 得,
得, ![]()
當![]() 時,因為
時,因為![]() ,所以
,所以![]() 顯然不成立,因此
顯然不成立,因此![]() .
.
令![]() ,則
,則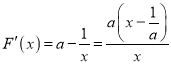 ,令
,令![]() ,得
,得![]() .
.
當![]() 時,
時, ![]() ,
, ![]() ,∴
,∴![]() ,所以
,所以![]() ,即有
,即有![]() .
.
因此![]() 時,
時, ![]() 在
在![]() 上恒成立.
上恒成立.
②當![]() 時,
時, ![]() ,
, ![]() 在
在![]() 上為減函數,在
上為減函數,在![]() 上為增函數,
上為增函數,
∴![]() ,不滿足題意.
,不滿足題意.
綜上,不等式![]() 在
在![]() 上恒成立時,實數
上恒成立時,實數![]() 的取值范圍是
的取值范圍是![]() .
.
(III)證明:由![]() 知數列
知數列![]() 是
是![]() 的等差數列,所以
的等差數列,所以![]()
所以![]()
由(Ⅱ)得, ![]() 在
在![]() 上恒成立.
上恒成立.
所以![]() . 將以上各式左右兩邊分別相加,得
. 將以上各式左右兩邊分別相加,得
![]() .因為
.因為![]()
所以![]()
所以![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 是矩形,面
是矩形,面![]() 底面
底面![]() ,且
,且![]() 是邊長為
是邊長為![]() 的等邊三角形,
的等邊三角形, ![]() 在
在![]() 上,且
上,且![]() 面
面![]() .
.

(1)求證: ![]() 是
是![]() 的中點;
的中點;
(2)在![]() 上是否存在點
上是否存在點![]() ,使二面角
,使二面角![]() 為直角?若存在,求出
為直角?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人各進行3次射擊,甲每次擊中目標的概率為![]() ,乙每次擊中目標的概率為
,乙每次擊中目標的概率為![]() 。
。
(1)記甲擊中目標的次數為![]() ,求
,求![]() 的概率分布及數學期望;
的概率分布及數學期望;
(2)求乙至多擊目標2次的概率;
(3)求甲恰好比乙多擊中目標2次的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某學校高三年級800名學生中隨機抽取50名測量身高,據測量被抽取的學生的身高全部介于155cm和195cm之間,將測量結果按如下方式分成八組:第一組[155,160);第二組[160,165);…第八組[190,195],圖是按上述分組方法得到的條形圖.

(1)根據已知條件填寫將表格填寫完整;
組別 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
樣本 | 2 | 4 | 10 | 10 | 15 | 4 |
(2)估計這所學校高三年級800名學生中身高在180cm以上(含180cm)的人數;
(3)在樣本中,若第二組有1人為男生,其余為女生,第七組有1人為女生,其余為男生,在第二組和第七組中各選一名同學組成實驗小組,問:實驗小組中恰為一男一女的概率是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年2月22日.在平昌冬奧會短道速滑男子500米比賽中.中國選手武大靖以連續打破世界紀錄的優異表現,為中國代表隊奪得了本屆冬奧會的首枚金牌,也創造中國男子冰上競速項目在冬奧會金牌零的突破.某高校為調查該校學生在冬奧會期間累計觀看冬奧會的時間情況.收集了200位男生、100位女生累計觀看冬奧會時間的樣本數據(單位:小時).又在100位女生中隨機抽取20個人.已知這20位女生的數據莖葉圖如圖所示.
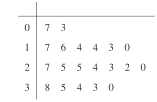
(1)將這20位女生的時間數據分成8組,分組區間分別為![]() ,在答題卡上完成頻率分布直方圖;
,在答題卡上完成頻率分布直方圖;
(2)以(1)中的頻率作為概率,求1名女生觀看冬奧會時間不少于30小時的概率;
(3)以(1)中的頻率估計100位女生中累計觀看時間小于20個小時的人數.已知200位男生中累計觀看時間小于20小時的男生有50人請完成答題卡中的列聯表,并判斷是否有99 %的把握認為“該校學生觀看冬奧會累計時間與性別有關”.
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
附:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】菜農定期使用低害殺蟲農藥對蔬菜進行噴灑,以防止害蟲的危害,但采集上市時蔬菜仍存有少量的殘留農藥,食用時需要用清水清洗干凈。假設1千克該蔬菜用清水![]() 千克清洗后,蔬菜上殘留的農藥為
千克清洗后,蔬菜上殘留的農藥為![]() 微克,通過樣本數據得到
微克,通過樣本數據得到![]() 關于
關于![]() 的散點圖。由數據分析可用函數
的散點圖。由數據分析可用函數![]() 擬合
擬合![]() 與
與![]() 的關系.
的關系.

(1)求![]() 與
與![]() 的回歸方程
的回歸方程![]() (
(![]() 精確到0.1);
精確到0.1);
(2)已知對于殘留在蔬菜上的農藥,當它的殘留量不超過20微克時對人體無害。為了放心食用該蔬菜,請估計至少需要用多少克的清水清洗1千克蔬菜?(答案精確到0.1)
附:①參考數據:![]() ,
,![]() ,
,![]() (其中
(其中![]() ),
),![]() 。
。
②參考公式:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區2011年至2017年農村居民家庭人均純收入(單位:千元)的數據如下表:

(I)求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(II)利用(I)中所求的線性回歸方程,分析該地區2011年至2017年農村居民家庭人均純收入的變化情況,并預測該地區2018年農村居民家庭人均純收入.
參考公式: .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校為“中學數學聯賽”選拔人才,分初賽和復賽兩個階段進行,規定:分數不小于本次考試成績中位數的具有復賽資格,某校有900名學生參加了初賽,所有學生的成績均在區間![]() 內,其頻率分布直方圖如圖.
內,其頻率分布直方圖如圖.

(1)求獲得復賽資格應劃定的最低分數線;
(2)從初賽得分在區間![]() 的參賽者中,利用分層抽樣的方法隨機抽取7人參加學校座談交流,那么從得分在區間
的參賽者中,利用分層抽樣的方法隨機抽取7人參加學校座談交流,那么從得分在區間![]() 與
與![]() 各抽取多少人?
各抽取多少人?
(3)從(2)抽取的7人中,選出4人參加全市座談交流,設![]() 表示得分在
表示得分在![]() 中參加全市座談交流的人數,學校打算給這4人一定的物質獎勵,若該生分數在
中參加全市座談交流的人數,學校打算給這4人一定的物質獎勵,若該生分數在![]() 給予500元獎勵,若該生分數在
給予500元獎勵,若該生分數在![]() 給予800元獎勵,用Y表示學校發的獎金數額,求Y的分布列和數學期望。
給予800元獎勵,用Y表示學校發的獎金數額,求Y的分布列和數學期望。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com