
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 是矩形,面
是矩形,面![]() 底面
底面![]() ,且
,且![]() 是邊長為
是邊長為![]() 的等邊三角形,
的等邊三角形, ![]() 在
在![]() 上,且
上,且![]() 面
面![]() .
.

(1)求證: ![]() 是
是![]() 的中點;
的中點;
(2)在![]() 上是否存在點
上是否存在點![]() ,使二面角
,使二面角![]() 為直角?若存在,求出
為直角?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
【答案】(1) 見解析;(2) ![]() .
.
【解析】試題分析:(1)連![]() 交
交![]() 于
于![]() 可得
可得![]() 是
是![]() 中點,再根據
中點,再根據![]() 面
面![]() 可得
可得![]() 進而根據中位線定理可得結果;(2)取
進而根據中位線定理可得結果;(2)取![]() 中點
中點![]() ,由(1)知
,由(1)知![]() 兩兩垂直. 以
兩兩垂直. 以![]() 為原點,
為原點, ![]() 所在直線分別為
所在直線分別為![]() 軸,
軸, ![]() 軸,
軸, ![]() 軸建立空間直角坐標系,求出面
軸建立空間直角坐標系,求出面![]() 的一個法向量
的一個法向量![]() ,用
,用![]() 表示面
表示面![]() 的一個法向量
的一個法向量![]() ,由
,由![]() 可得結果.
可得結果.
試題解析:(1)證明:連![]() 交
交![]() 于
于![]() ,連
,連![]() 是矩形,
是矩形, ![]() 是
是![]() 中點.又
中點.又![]() 面
面![]() ,且
,且![]() 是面
是面![]() 與面
與面![]() 的交線,
的交線, ![]() 是
是![]() 的中點.
的中點.
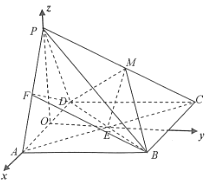
(2)取![]() 中點
中點![]() ,由(1)知
,由(1)知![]() 兩兩垂直. 以
兩兩垂直. 以![]() 為原點,
為原點, ![]() 所在直線分別為
所在直線分別為![]() 軸,
軸,
![]() 軸,
軸, ![]() 軸建立空間直角坐標系(如圖),則各點坐標為
軸建立空間直角坐標系(如圖),則各點坐標為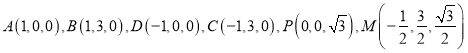 .
.
設存在![]() 滿足要求,且
滿足要求,且![]() ,則由
,則由![]() 得:
得: ![]() ,面
,面![]() 的一個法向量為
的一個法向量為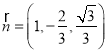 ,面
,面![]() 的一個法向量為
的一個法向量為![]() ,由
,由![]() ,得
,得![]() ,解得
,解得![]() ,故存在
,故存在![]() ,使二面角
,使二面角![]() 為直角,此時
為直角,此時![]() .
.


科目:高中數學 來源: 題型:
【題目】已知小張每次射擊命中十環的概率都為40%,現采用隨機模擬的方法估計小張三次射擊恰有兩次命中十環的概率,先由計算器產生0到9之間取整數值的隨機數,指定2,4,6,8表示命中十環,0,1,3,5,7,9表示未命中十環,再以每三個隨機數為一組,代表三次射擊的結果,經隨機模擬產生了如下20組隨機數:
321 421 292 925 274 632 800 478 598 663 531 297 396
021 506 318 230 113 507 965
據此估計,小張三次射擊恰有兩次命中十環的概率為()
A. 0.25B. 0.30C. 0.35D. 0.40
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》里有一段敘述:今有良馬與駑馬發長安至齊,齊去長安一千一百二十五里,良馬初日行一百零三里,日增十三里;駑馬初日行九十七里,日減半里;良馬先至齊,復還迎駑馬,二馬相逢.根據該問題設計程序框圖如下,若輸入![]() ,則輸出
,則輸出![]() 的值是( )
的值是( )
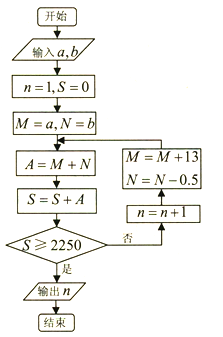
A. 8 B. 9 C. 12 D. 16
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列四個命題中,其中錯誤的個數是()
①經過球面上任意兩點,可以作且只可以作一個大圓;
②經過球直徑的三等分點,作垂直于該直徑的兩個平面,則這兩個平面把球面分成三部分的面積相等;
③球的面積是它大圓面積的四倍;
④球面上兩點的球面距離,是這兩點所在截面圓上,以這兩點為端點的劣弧的長.
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】時下,租車自駕游已經比較流行了.某租車點的收費標準為:不超過![]() 天收費
天收費![]() 元,超過
元,超過![]() 天的部分每天收費
天的部分每天收費![]() 元(不足
元(不足![]() 天按
天按![]() 天計算).甲、乙兩人要到該租車點租車自駕到某景區游覽,他們不超過
天計算).甲、乙兩人要到該租車點租車自駕到某景區游覽,他們不超過![]() 天還車的概率分別為
天還車的概率分別為![]() 和
和![]() ,
,![]() 天以上且不超過
天以上且不超過![]() 天還車的概率分別為
天還車的概率分別為![]() 和
和![]() ,兩人租車都不會超過
,兩人租車都不會超過![]() 天.
天.
(1)求甲所付租車費比乙多的概率;
(2)設甲、乙兩人所付的租車費之和為隨機變量![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】f(x)的定義域為(0,+∞),且對一切x>0,y>0都有f![]() =f(x)-f(y),當x>1時,有f(x)>0。
=f(x)-f(y),當x>1時,有f(x)>0。
(1)求f(1)的值;
(2)判斷f(x)的單調性并證明;
(3)若f(6)=1,解不等式f(x+3)-f![]() <2;
<2;
(4)若f(4)=2,求f(x)在[1,16]上的值域。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在R上的函數f(x)=2x-![]() .
.
(1)若f(x)=![]() ,求x的值;
,求x的值;
(2)若2tf(2t)+mf(t)≥0對于t∈[1,2]恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的焦點曲線
的焦點曲線![]() 的一個焦點,
的一個焦點, ![]() 為坐標原點,點
為坐標原點,點![]() 為拋物線
為拋物線![]() 上任意一點,過點
上任意一點,過點![]() 作
作![]() 軸的平行線交拋物線的準線于
軸的平行線交拋物線的準線于![]() ,直線
,直線![]() 交拋物線于點
交拋物線于點![]() .
.
(Ⅰ)求拋物線![]() 的方程;
的方程;
(Ⅱ)求證:直線![]() 過定點
過定點![]() ,并求出此定點的坐標.
,并求出此定點的坐標.
【答案】(I)![]() ;(II)證明見解析.
;(II)證明見解析.
【解析】試題分析:(Ⅰ)將曲線![]() 化為標準方程,可求得
化為標準方程,可求得![]() 的焦點坐標分別為
的焦點坐標分別為![]() ,可得
,可得![]() ,所以
,所以![]() ,即拋物線的方程為
,即拋物線的方程為![]() ;(Ⅱ)結合(Ⅰ),可設
;(Ⅱ)結合(Ⅰ),可設![]() ,得
,得 ,從而直線
,從而直線![]() 的方程為
的方程為![]() ,聯立直線與拋物線方程得
,聯立直線與拋物線方程得![]() ,解得
,解得![]() ,直線
,直線![]() 的方程為
的方程為 ,整理得
,整理得![]() 的方程為
的方程為![]() ,此時直線恒過定點
,此時直線恒過定點![]() .
.
試題解析:(Ⅰ)由曲線![]() ,化為標準方程可得
,化為標準方程可得 , 所以曲線
, 所以曲線 是焦點在
是焦點在![]() 軸上的雙曲線,其中
軸上的雙曲線,其中![]() ,故
,故![]() ,
, ![]() 的焦點坐標分別為
的焦點坐標分別為![]() ,因為拋物線的焦點坐標為
,因為拋物線的焦點坐標為![]() ,由題意知
,由題意知![]() ,所以
,所以![]() ,即拋物線的方程為
,即拋物線的方程為![]() .
.
(Ⅱ)由(Ⅰ)知拋物線![]() 的準線方程為
的準線方程為![]() ,設
,設![]() ,顯然
,顯然![]() .故
.故 ,從而直線
,從而直線![]() 的方程為
的方程為![]() ,聯立直線與拋物線方程得
,聯立直線與拋物線方程得![]() ,解得
,解得![]()
①當![]() ,即
,即![]() 時,直線
時,直線![]() 的方程為
的方程為![]() ,
,
②當![]() ,即
,即![]() 時,直線
時,直線![]() 的方程為
的方程為 ,整理得
,整理得![]() 的方程為
的方程為![]() ,此時直線恒過定點
,此時直線恒過定點![]() ,
, ![]() 也在直線
也在直線![]() 的方程為
的方程為![]() 上,故直線
上,故直線![]() 的方程恒過定點
的方程恒過定點![]() .
.
【題型】解答題
【結束】
21
【題目】已知函數![]() ,
, ![]()
(Ⅰ)當![]() 時,求函數
時,求函數![]() 的單調遞減區間;
的單調遞減區間;
(Ⅱ)若![]() 時,關于
時,關于![]() 的不等式
的不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(Ⅲ)若數列![]() 滿足
滿足![]() ,
, ![]() ,記
,記![]() 的前
的前![]() 項和為
項和為![]() ,求證:
,求證: ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com