Question

19．實數x，y滿足不等式組$\left\{\begin{array}{l}x≥0\\ y≥0\\ x-y-1≤0\\ x-2y+1≥0\end{array}\right.$，則2x-y的最大值為（　　）

• A． $-\frac{1}{2}$
• B． 0
• C． 2
• D． 4

Answer 1

分析 作出不等式組對應的平面區域，利用目標函數k的幾何意義，進行平移，結合圖象得到k=2x-y的最大值．

解答 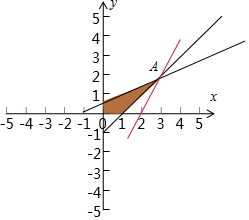解：作出不等式組對應的平面區域如圖：（陰影部分）．
由k=2x-y得y=2x-k，
平移直線y=2x-k，
由圖象可知當直線y=2x-k經過點A時，直線y=2x-k的截距最小，
此時k最大．
由$\left\{\begin{array}{l}{x-y-1=0}\\{x-2y+1=0}\end{array}\right.$可得A（3，2），標代入目標函數k=2×3-2=4，
即k=2x-y的最大值為4．
故選：D．

點評 本題主要考查線性規劃的應用，利用數形結合是解決此類問題的基本方法，利用k的幾何意義是解決本題的關鍵．