
| A. | (1,2) | B. | (-$\frac{1}{2}$,2) | C. | (-2,2) | D. | (-3,2) |
分析 根據不等式x2-2ax+a>0恒成立△<0,求出0<a<1;把不等式a2x+1<a${\;}^{{x}^{2}+2x-3}$<1化為2x+1>x2+2x-3>0,求出它的解集即可.
解答 解:不等式x2-2ax+a>0(x∈R)恒成立,則△<0,
∴4a2-4a<0,
解得0<a<1;
∴不等式a2x+1<a${\;}^{{x}^{2}+2x-3}$<1可化為:
2x+1>x2+2x-3>0,
即$\left\{\begin{array}{l}{2x+1{>x}^{2}+2x-3}\\{{x}^{2}+2x-3>0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{-2<x<2}\\{x<-3或x>1}\end{array}\right.$
解得1<x<2,
所以不等式的解集是(1,2).
故選:A.
點評 本題考查了不等式恒成立問題以及指數函數的性質與應用問題,是基礎題目.


科目:高中數學 來源: 題型:選擇題
| A. | 既是等差數列又是等比數列 | B. | 既不是等差數列也不是等比數列 | ||
| C. | 是等差數列但不是等比數列 | D. | 是等比數列但不是等差數列 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -3 | B. | -2 | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(x)=x0與f(x)=1 | B. | f(x)=$\sqrt{{x}^{2}}$-1與f(x)=|x|-1 | ||
| C. | f(x)=$\frac{{x}^{2}-4}{x+2}$與f(x)=x-2 | D. | f(x)=$\sqrt{(x-1)(x-2)}$與f(x)=$\sqrt{x-1}$$\sqrt{x-2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
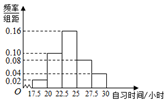 某中學調查200名學生每周晚自習時間(單位,小時),制成了如圖所示頻率分布直方圖,其中自習時間的范圍為[17.5,30],根據直方圖,這200名學生每周自習時間不少于22.5小時的人數是140.
某中學調查200名學生每周晚自習時間(單位,小時),制成了如圖所示頻率分布直方圖,其中自習時間的范圍為[17.5,30],根據直方圖,這200名學生每周自習時間不少于22.5小時的人數是140.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com