Question

已知f（x）為奇函數，且x＞0時，f（x）=2^x-1-2，
（1）求x＜0時，f（x）的解析式；
（2）畫出f（x）的圖象；
（3）寫出f（x）的單調區間．

Answer 1

考點：函數圖象的作法,函數解析式的求解及常用方法,函數單調性的判斷與證明

專題：函數的性質及應用

分析：（1）利用函數的奇偶性求當x＜0時，f（x）的解析式；
（2）先畫當x＞0時的圖象：f（x）=2^x-1-2，此函數可由指數函數y=2x先向右平移1個單位，再向下平移2個單位；
再根據圖象關于原點對稱畫出當x＞0時的圖象，另外，f（0）=0；
（3）利用函數的圖象，判斷函數的單調區間．

解答： 解：設x＜0，則-x＞0，
∵當x＞0時，f（x）=2^x-1-2，
∴f（-x）=2^-x-1-2，
又∵函數f（x）是定義在R上的奇函數，
∴f（-x）=-f（x），∴f（x）=-f（-x）=-2^-x-1+2，
∴當x＜0時，f（x）=-2^-x-1+2，
（2）先畫當x＞0時的圖象：f（x）=2^x-1-2，此函數可由指數函數y=2x先向右平移1個單位，再向下平移2個單位；
再根據圖象關于原點對稱畫出當x＞0時的圖象，另外，f（0）=0，圖象如下：

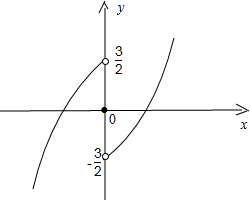
（3）由圖象可知，函數的單調增區間為（-∞，0）、（0，+∞）．

點評：本題主要考查函數奇偶性的應用，以及函數單調性的判斷，考查函數的綜合性質的應用．