
分析 (1)直線y=mx+1過定點(0,1),且在橢圓的內部,可得結論;
(2)直線y=mx+1過定點(0,1),設A(x1,y1),B(x2,y2),則OP的中點M為($\frac{x}{2}$,$\frac{y}{2}$),且有2x12+y12=2,2x22+y22=2,由此能求出點P的軌跡方程.
(3)假設存在直線l,使OAPB為矩形.由于OA⊥OB,則有x1x2+y1y2=0,運用韋達定理及點在直線上滿足直線方程,化簡整理得到的方程,解出m,注意檢驗判別式是否大于0.
解答 (1)證明:直線y=mx+1過定點(0,1),且在橢圓的內部,
∴橢圓C:ax2+y2=2(a>0)與直線L:y=mx+1總有兩個交點.
(2)解:設A(x1,y1),B(x2,y2),
則OP的中點M為($\frac{x}{2}$,$\frac{y}{2}$),
且有2x12+y12=2,2x22+y22=2,
以上兩式相減,得kAB•kOP=-2,
∴$\frac{\frac{y}{2}-1}{\frac{x}{2}}•\frac{y}{x}$=-2,
∴2x2+y2-2y=0,
點P的軌跡方程為2x2+(y-1)2=1(除去原點).
(3)解:由直線與橢圓聯立,得(a+m2)x2+2mx-1=0,
∴x1+x2=-$\frac{2m}{a+{m}^{2}}$,x1x2=-$\frac{1}{a+{m}^{2}}$,
y1y2=(mx1+1)(mx2+1)=m2x1x2+m(x1+x2)+1=$\frac{a-2{m}^{2}}{a+{m}^{2}}$,
由于OA⊥OB,則有x1x2+y1y2=0,即為-$\frac{1}{a+{m}^{2}}$+$\frac{a-2{m}^{2}}{a+{m}^{2}}$=0,
解得,a=2m2-1.
檢驗:判別式△>0,成立.
故存在直線l:y=±$\sqrt{\frac{a+1}{2}}$(x+1),使OAPB為矩形.
點評 本題主要考查直線與圓錐曲線的綜合應用能力,具體涉及到軌跡方程的求法及直線與橢圓的相關知識,解題時要注意合理地進行等價轉化.


科目:高中數學 來源: 題型:解答題
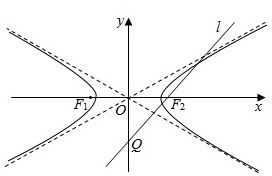 如圖,雙曲線Γ:$\frac{{x}^{2}}{3}$-y2=1的左、右焦點分別為F1,F2,過F2作直線l交y軸于點Q.
如圖,雙曲線Γ:$\frac{{x}^{2}}{3}$-y2=1的左、右焦點分別為F1,F2,過F2作直線l交y軸于點Q.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -1 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | sinα=$\frac{3}{5}$ | B. | cosα=-$\frac{4}{5}$ | C. | tanα=-$\frac{3}{4}$ | D. | tanα=-$\frac{4}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 5 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com