Question

1．某校高三（1）班的一次數學測試成績的莖葉圖和頻率分布直方圖都受到不同程度的破壞，但可見部分如下，據此解答如下問題．

（1）求全班人數及分數在[80，90）之間的頻數，并估計該班的平均分數；
（2）若要從分數在[80，100]之間的試卷中任取兩份分析學生失分情況，在抽取的試卷中，求至少有一份分數在[90，100]之間的概率．

Answer 1

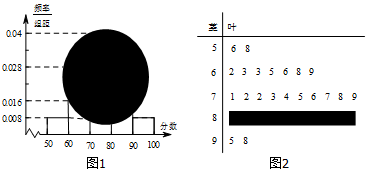
分析 （1）由莖葉圖，利用頻數、頻率與樣本容量的關系求出全班人數，計算該班的平均分；
（2）利用列舉法求出基本事件數，計算對應的概率值．

解答 解：（1）由莖葉圖知，分數在[50，60）之間的頻數為2，
頻率為0.008×10=0.08，全班人數為$\frac{2}{0.08}=25$；
所以分數在[80，90）之間的頻數為25-2-7-10-2=4，
分數在[50，60）之間的總分為56+58=114；
分數在[60，70）之間的總分為60×7+2+3+3+5+6+8+9=456；
分數在[70，80）之間的總分數為70×10+1+2+3+3+4+5+6+7+8+9=747；
分數在[80，90）之間的總分約為85×4=340；
分數在[90，100]之間的總分數為95+98=193；
所以，該班的平均分數為$\frac{114+456+747+340+193}{25}=74$；
（2）將[80，90）之間的4個分數編號為1，2，3，4，[90，100]之間的2個分數編號為5，6，
在[80，100]之間的試卷中任取兩份的基本事件為：
（1，2），（1，3），（1，4），（1，5），（1，6），
（2，3），（2，4），（2，5），（2，6），
（3，4），（3，5），（3，6），
（4，5），（4，6），（5，6）共15個，
其中，至少有一個在[90，100]之間的基本事件有9個，
∴至少有一份分數在[90，100]之間的概率是$\frac{9}{15}=0.6$．

點評 本題考查了莖葉圖與頻率分布直方圖的應用問題，也考查了用列舉法求古典概型的概率問題，是綜合性題目．