
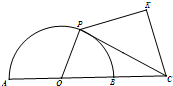
 如圖,已知半圓O的半徑為1,點C在直徑AB的延長線上,且BC=1,P是半圓上動點,以PC為一邊作等腰直角三角形PCK(K為直角頂點,且K和O在PC的兩側).
如圖,已知半圓O的半徑為1,點C在直徑AB的延長線上,且BC=1,P是半圓上動點,以PC為一邊作等腰直角三角形PCK(K為直角頂點,且K和O在PC的兩側).分析 (1)可以設∠POB=θ,四邊形面積為y,然后,建立關系式,構造面積關系式,最后利用三角函數知識求解最值;
(2)由t=$\frac{△POC的面積}{△PCK的面積}$=$\frac{4sinθ}{5-4cosθ}$,由半角公式及同角三角函數基本關系,求得t═$\frac{8tan\frac{θ}{2}}{9ta{n}^{2}\frac{θ}{2}+1}$=$\frac{8}{9tan\frac{θ}{2}+\frac{1}{tan\frac{θ}{2}}}$≤$\frac{8}{2×\sqrt{9tan\frac{θ}{2}•\frac{1}{tan\frac{θ}{2}}}}$=$\frac{4}{3}$,即可求得t的最大值.
解答 解:(1)設∠POC=θ,0<θ<π,
則在△POC中,由余弦定理得:PC2=OP2+OC2-2OP•OCcosθ=5-4cosθ.
∴PC2=5-4cos θ,…(4分)
SOPKC=S△OPC+S△PCD=$\frac{1}{2}$×1×2sinθ+$\frac{\sqrt{3}}{4}$(5-4cosθ)
=2sin(θ-$\frac{π}{3}$)+$\frac{5\sqrt{3}}{4}$,
當θ-$\frac{π}{3}$=$\frac{π}{2}$,即θ=$\frac{5π}{6}$時,四邊形OPKC面積的最大值;,
最大值為:2+$\frac{5\sqrt{3}}{4}$;
(2)t=$\frac{△POC的面積}{△PCK的面積}$,
=$\frac{4sinθ}{5-4cosθ}$,
=$\frac{8sin\frac{θ}{2}cos\frac{θ}{2}}{5(si{n}^{2}\frac{θ}{2}+co{s}^{2}\frac{θ}{2})-4(co{s}^{2}\frac{θ}{2}-si{n}^{2}\frac{θ}{2})}$,
=$\frac{8sin\frac{θ}{2}cos\frac{θ}{2}}{9si{n}^{2}\frac{θ}{2}+co{s}^{2}\frac{θ}{2}}$,
=$\frac{8tan\frac{θ}{2}}{9ta{n}^{2}\frac{θ}{2}+1}$,
=$\frac{8}{9tan\frac{θ}{2}+\frac{1}{tan\frac{θ}{2}}}$≤$\frac{8}{2×\sqrt{9tan\frac{θ}{2}•\frac{1}{tan\frac{θ}{2}}}}$=$\frac{4}{3}$,
當且僅當tan$\frac{θ}{2}$=$\frac{1}{3}$時,取“=”,
t的最大值為:$\frac{4}{3}$,
點評 本題重點考查了三角函數的輔助角公式、三角恒等變換等知識,基本不等式的綜合應用,考查計算能力,屬于中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | A=B | B. | A?B | C. | B?A | D. | A∩B=∅ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a<b<c | B. | b<c<a | C. | b<a<c | D. | c<a<b |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $y=sin(4x-\frac{π}{5})$ | B. | $y=sin(2x-\frac{2π}{5})$ | C. | $y=sin(4x-\frac{2π}{5})$ | D. | $y=sin(4x-\frac{3π}{5})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 192種 | B. | 216種 | C. | 240種 | D. | 360種 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com