
 有一塊半徑為R(R為正常數)的半圓形空地,開發商計劃征地建一個游泳池ABCD和其附屬設施,附屬設施占地形狀是等腰△CDE,其中O為圓心,A,B在圓的直徑上,C,D,E在半圓周上,如圖.
有一塊半徑為R(R為正常數)的半圓形空地,開發商計劃征地建一個游泳池ABCD和其附屬設施,附屬設施占地形狀是等腰△CDE,其中O為圓心,A,B在圓的直徑上,C,D,E在半圓周上,如圖.分析 (1)連結OC,OE,用θ表示出BC,OB,代入梯形面積公式即可得出f(θ);
(2)令sinθ+cosθ=t,使用換元法求出g(θ)的最值及對應的θ.
解答 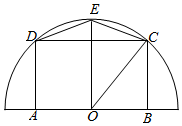 解:(1)連結OE,OC,
解:(1)連結OE,OC,
在Rt△OBC中,BC=Rsinθ,OB=Rcosθ,
∴S梯形OBCE=$\frac{1}{2}$(Rsinθ+R)Rcosθ=$\frac{1}{2}$R2(1+sinθ)cosθ,
∴f(θ)=2S梯形OBCE=R2(1+sinθ)cosθ,θ∈(0,$\frac{π}{2}$).
(2)g(θ)=R2(1+sinθ)cosθ+R2sinθ=R2(sinθ+cosθ+sinθcosθ),
令t=sinθ+cosθ=$\sqrt{2}$sin(θ+$\frac{π}{4}$),則t∈(1,$\sqrt{2}$],sinθcosθ=$\frac{{t}^{2}-1}{2}$,
∴g(θ)=R2($\frac{{t}^{2}-1}{2}+t$)=$\frac{{R}^{2}}{2}$[(t+1)2-2],
令h(t)=$\frac{{R}^{2}}{2}$[(t+1)2-2],則h(t)在(1,$\sqrt{2}$]上單調遞增,
∴當t=$\sqrt{2}$即θ=$\frac{π}{4}$時,h(t)取得最大值($\frac{1}{2}+\sqrt{2}$)R2,
點評 本題考查了函數模型的應用,函數最值的計算,屬于中檔題.


 期末1卷素質教育評估卷系列答案
期末1卷素質教育評估卷系列答案科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
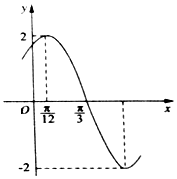 已知函數f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分圖象如圖所示,下列說法正確的是( )
已知函數f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分圖象如圖所示,下列說法正確的是( )| A. | 函數f(x)的圖象關于直線x=-$\frac{2π}{3}$對稱 | |
| B. | 函數f(x)的圖象關于點(-$\frac{11π}{12}$,0)對稱 | |
| C. | 若方程f(x)=m在[-$\frac{π}{2}$,0]上有兩個不相等的實數根,則實數m∈(-2,-$\sqrt{3}$] | |
| D. | 將函數f(x)的圖象向左平移$\frac{π}{6}$個單位可得到一個偶函數 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com