
分析 (Ⅰ)曲線C的極坐標方程化為ρ2-4ρcosθ+3ρ2sin2θ=0,由此能求出曲線C的直角坐標方程;由直線l過點M(1,0),傾斜角為$\frac{π}{6}$,能求出直線l的參數方程.
(Ⅱ)由曲線C經過伸縮變換$\left\{\begin{array}{l}{x′=x}\\{y′=2y}\end{array}\right.$后得到曲線C′,求出曲線C′為:(x-2)2+y2=4,把直線l的參數方程代入曲線C′,得:${t}^{2}-\sqrt{3}t-3=0$,設A,B對應的參數分別為t1,t2,則t1+t2=$\sqrt{3}$,t1t2=-3,由此能求出|MA|+|MB|.
解答 解:(Ⅰ)∵曲線C的極坐標方程為ρ-4cosθ+3ρsin2θ=0,∴ρ2-4ρcosθ+3ρ2sin2θ=0,
∴曲線C的直角坐標方程為x2+y2-4x+3y2=0,整理,得(x-2)2+4y2=4,
∵直線l過點M(1,0),傾斜角為$\frac{π}{6}$,
∴直線l的參數方程為$\left\{\begin{array}{l}{y=1+tcos\frac{π}{6}}\\{y=tsin\frac{π}{6}}\end{array}\right.$,即$\left\{\begin{array}{l}{x=1+\frac{\sqrt{3}}{2}t}\\{y=\frac{1}{2}t}\end{array}\right.$,(t是參數).
(Ⅱ)∵曲線C經過伸縮變換$\left\{\begin{array}{l}{x′=x}\\{y′=2y}\end{array}\right.$后得到曲線C′,
∴曲線C′為:(x-2)2+y2=4,
把直線l的參數方程$\left\{\begin{array}{l}{x=1+\frac{\sqrt{3}}{2}t}\\{y=\frac{1}{2}t}\end{array}\right.$,(t是參數)代入曲線C′:(x-2)2+y2=4,得:
${t}^{2}-\sqrt{3}t-3=0$,
設A,B對應的參數分別為t1,t2,則t1+t2=$\sqrt{3}$,t1t2=-3,
∴|MA|+|MB|=|t1|+|t2|=|t1-t2|=$\sqrt{({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}}$=$\sqrt{3+12}$=$\sqrt{15}$.
點評 本題考查曲線的直角坐標方程與直線的參數方程的求法,考查兩線段和的求法,涉及到直角坐標方程、極坐標方程、參數方程的互化、韋達定理等基礎知識,考查推理論證能力、運算求解能力,考查化歸與轉化思想、函數與方程思想,是中檔題.


 活力課時同步練習冊系列答案
活力課時同步練習冊系列答案 學業測評一課一測系列答案
學業測評一課一測系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\overline{x}$=μ | B. | $\overline{x}$≈μ | C. | μ是$\overline{x}$的估計值 | D. | $\overline{x}$是μ的估計值 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
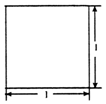 若一個底面是等腰直角三角形的直三棱柱的正視圖如圖所示,其頂點都在一個球面上,則該球的表面積為( )
若一個底面是等腰直角三角形的直三棱柱的正視圖如圖所示,其頂點都在一個球面上,則該球的表面積為( )| A. | 6π或5π | B. | 3π或5π | C. | 6π | D. | 5π |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 直線 | B. | 圓 | C. | 橢圓 | D. | 雙曲線 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{2\sqrt{2}}{3}$或$\frac{4\sqrt{2}}{9}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{7\sqrt{2}}{8}$ | D. | $\frac{\sqrt{2}}{4}$或$\frac{7\sqrt{2}}{8}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
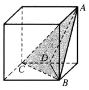 如圖是一個正方體,A,B,C為三個頂點,D是棱的中點,則三棱錐A-BCD的正視圖,俯視圖是(注:選項中的上圖是正視圖,下圖是俯視圖)( )
如圖是一個正方體,A,B,C為三個頂點,D是棱的中點,則三棱錐A-BCD的正視圖,俯視圖是(注:選項中的上圖是正視圖,下圖是俯視圖)( )| A. | 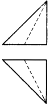 | B. | 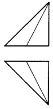 | C. | 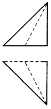 | D. | 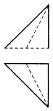 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (?p)∧q | B. | p∧q | C. | p∧(?q) | D. | p∨(?q) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com