日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

12．設函數(shù)f（x）=$\sqrt{x}$的反函數(shù)是f-1（x），則f-1（4）=16．

分析 先求出x=y2，y≥0，互換x，y，得f-1（x）=x2，x≥0，由此能求出f-1（4）．

解答 解：∵函數(shù)f（x）=y=$\sqrt{x}$的反函數(shù)是f-1（x），
∴x=y2，y≥0，
互換x，y，得f-1（x）=x2，x≥0，
∴f-1（4）=42=16．
故答案為：16．

點評 本題考查反函數(shù)的求法，是基礎題，解題時要認真審題，注意反函數(shù)性質(zhì)的合理運用．

練習冊系列答案
相關習題

科目：高中數(shù)學 來源： 題型：解答題

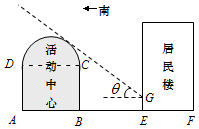2．如圖所示，某街道居委會擬在EF地段的居民樓正南方向的空白地段AE上建一個活動中心，其中AE=30米．活動中心東西走向，與居民樓平行．從東向西看活動中心的截面圖的下部分是長方形ABCD，上部分是以DC為直徑的半圓．為了保證居民樓住戶的采光要求，活動中心在與半圓相切的太陽光線照射下落在居民樓上的影長GE不超過2.5米，其中該太陽光線與水平線的夾角θ滿足$tanθ=\frac{3}{4}$．
（1）若設計AB=18米，AD=6米，問能否保證上述采光要求？
（2）在保證上述采光要求的前提下，如何設計AB與AD的長度，可使得活動中心的截面面積最大？（注：計算中π取3）

查看答案和解析>>

科目：高中數(shù)學 來源： 題型：選擇題

3．$cos\frac{2017π}{3}$等于（　　）
A．$-\frac{1}{2}$B．$\frac{1}{2}$C．$-\frac{{\sqrt{3}}}{2}$D．$\frac{{\sqrt{3}}}{2}$

查看答案和解析>>

科目：高中數(shù)學 來源： 題型：解答題

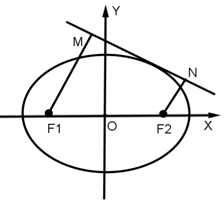20．已知橢圓C的方程是$\frac{x^2}{4}+\frac{y^2}{3}=1$，直線l：y=kx+m與橢圓C有且僅有一個公共點，若F1M⊥l，F(xiàn)2N⊥l，M，N分別為垂足．
（Ⅰ）證明：$|{{F_1}M}|+|{{F_2}N}|≥2\sqrt{3}$；
（Ⅱ）求四邊形F1MNF2面積S的最大值．

查看答案和解析>>

科目：高中數(shù)學 來源： 題型：填空題

7．已知圓C：x2+y2-2x+4y=0，則圓C的半徑為$\sqrt{5}$，過點（2，1）的直線中，被圓C截得弦長最長的直線方程為3x-y-5=0．

查看答案和解析>>

科目：高中數(shù)學 來源： 題型：解答題

17．某同學用“五點法”畫函數(shù)f（x）=Asin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）在某一個周期內(nèi)的圖象時，列表并填入了部分數(shù)據(jù)，如表：
ωx+φ 0$\frac{π}{2}$  π$\frac{3π}{2}$  2π
 x-$\frac{π}{12}$ $\frac{π}{6}$$\frac{5π}{12}$ $\frac{2π}{3}$$\frac{11π}{12}$
 f（x）0  30 -30 
（1）請將表中數(shù)據(jù)補充完整，并直接寫出函數(shù)f（x）的解析式；
（2）若將函數(shù)f（x）的圖象上所有點的橫坐標變?yōu)樵瓉淼?倍，縱坐標不變，得到函數(shù)g（x）的圖象，求當x∈[-$\frac{π}{3}$，$\frac{π}{3}$]時，函數(shù)g（x）的值域；
（3）若將y=f（x）圖象上所有點向左平移θ（θ＞0）個單位長度，得到y(tǒng)=h（x）的圖象，若=h（x）圖象的一個對稱中心為（$\frac{π}{12}，0$），求θ的最小值．

查看答案和解析>>

科目：高中數(shù)學 來源： 題型：選擇題

4．設F1，F(xiàn)2分別為雙曲線C：$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1（a＞0，b＞0）$的兩個焦點，M，N是雙曲線C的一條漸近線上的兩點，四邊形MF1NF2為矩形，A為雙曲線的一個頂點，若△AMN的面積為$\frac{1}{2}{c}^{2}$，則該雙曲線的離心率為（　　）
A．3B．2C．$\sqrt{3}$D．$\sqrt{2}$

查看答案和解析>>

科目：高中數(shù)學 來源： 題型：選擇題

1．如圖是函數(shù)f（x）=cos（πx+φ）（0＜φ＜$\frac{π}{2}$）的部分圖象，則f（3x0）=（　　）
A．$\frac{1}{2}$B．-$\frac{1}{2}$C．$\frac{\sqrt{3}}{2}$D．-$\frac{\sqrt{3}}{2}$

查看答案和解析>>

科目：高中數(shù)學 來源： 題型：選擇題

2．已知函數(shù)f（x）=$\left\{\begin{array}{l}{-x+a，x＜1}\\{{x}^{2}，x≥1}\end{array}\right.$存在最小值，則當實數(shù)a取最小值時，f[f（-2）]=（　　）
A．-2B．4C．9D．16

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 曰本少妇色xxxxx日本妇 | 中文字幕黄色 | 黄av在线播放 | 国产成人在线播放 | 欧美午夜精品一区二区三区 | 国产91免费在线 | 亚洲视频欧美视频 | 国精产品一区二区三区黑人免费看 | 精品久久国产 | 国产日皮视频 | 婷婷久久综合 | 亚洲精品国产setv | 国产欧美日本 | 91精品久久久久久久久入口 | 福利片免费观看 | 99爱在线观看 | 日韩精品专区在线影院重磅 | 这里只有精品在线 | 亚洲天堂av中文字幕 | 韩国精品视频在线观看 | 国产精品日韩专区 | 日本黄色一区 | 欧美日韩亚洲一区 | www黄| 日韩欧美一二三区 | 蜜桃久久| 久久精品小视频 | 欧美一区二区三区的 | 欧美一区久久 | 久久精品视 | 亚洲成人在线网站 | 久久精品这里只有精品 | 国产91网址 | 日韩精品免费看 | √新版天堂资源在线资源 | 成人a在线 | 中文字幕 欧美 日韩 | 国产一区二区精品在线 | 亚洲欧美日韩天堂 | 日韩久久午夜一级啪啪 | 欧美精品一区二区久久 |