
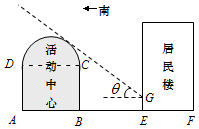
 如圖所示,某街道居委會擬在EF地段的居民樓正南方向的空白地段AE上建一個活動中心,其中AE=30米.活動中心東西走向,與居民樓平行.從東向西看活動中心的截面圖的下部分是長方形ABCD,上部分是以DC為直徑的半圓.為了保證居民樓住戶的采光要求,活動中心在與半圓相切的太陽光線照射下落在居民樓上的影長GE不超過2.5米,其中該太陽光線與水平線的夾角θ滿足$tanθ=\frac{3}{4}$.
如圖所示,某街道居委會擬在EF地段的居民樓正南方向的空白地段AE上建一個活動中心,其中AE=30米.活動中心東西走向,與居民樓平行.從東向西看活動中心的截面圖的下部分是長方形ABCD,上部分是以DC為直徑的半圓.為了保證居民樓住戶的采光要求,活動中心在與半圓相切的太陽光線照射下落在居民樓上的影長GE不超過2.5米,其中該太陽光線與水平線的夾角θ滿足$tanθ=\frac{3}{4}$.分析 (1)以點A為坐標原點,AB所在直線為x軸,建立平面直角坐標系.設太陽光線所在直線方程為$y=-\frac{3}{4}x+b$,利用直線與圓相切,求出直線方程,令x=30,得EG=1.5米<2.5米,即可得出結論;
(2)欲使活動中心內部空間盡可能大,則影長EG恰為2.5米,即可求出截面面積最大
解答 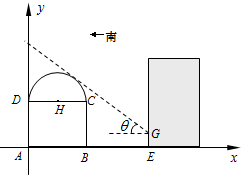 解:如圖所示,以點A為坐標原點,AB所在直線為x軸,建立平面直角坐標系.
解:如圖所示,以點A為坐標原點,AB所在直線為x軸,建立平面直角坐標系.
(1)因為AB=18,AD=6,所以半圓的圓心為H(9,6),
半徑r=9.設太陽光線所在直線方程為$y=-\frac{3}{4}x+b$,
即3x+4y-4b=0,…(2分)
則由$\frac{|27+24-4b|}{{\sqrt{{3^2}+{4^2}}}}=9$,
解得b=24或$b=\frac{3}{2}$(舍).
故太陽光線所在直線方程為$y=-\frac{3}{4}x+24$,…(5分)
令x=30,得EG=1.5米<2.5米.
所以此時能保證上述采光要求…(7分)
(2)設AD=h米,AB=2r米,則半圓的圓心為H(r,h),半徑為r.
欲使活動中心內部空間盡可能大,則影長EG恰為2.5米,則此時點G為(30,2.5),
設過點G的上述太陽光線為l1,則l1所在直線方程為y-$\frac{5}{2}$=-$\frac{3}{4}$(x-30),
即3x+4y-100=0…(10分)
由直線l1與半圓H相切,得$r=\frac{|3r+4h-100|}{5}$.
而點H(r,h)在直線l1的下方,則3r+4h-100<0,
即$r=-\frac{3r+4h-100}{5}$,從而h=25-2r…(13分)
又$S=2rh+\frac{1}{2}π{r^2}=2r(25-2r)+\frac{3}{2}×{r^2}$=$-\frac{5}{2}{r^2}+50r=-\frac{5}{2}{(r-10)^2}+250≤250$.
當且僅當r=10時取等號.
所以當AB=20米且AD=5米時,可使得活動中心的截面面積最大…(16分)
點評 本題考查利用數學知識解決實際問題,考查直線與圓的位置關系,考查配方法的運用,考查學生分析解決問題的能力,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com