
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | -$\frac{π}{12}$ | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{2π}{3}$ | $\frac{11π}{12}$ |
| f(x) | 0 | 3 | 0 | -3 | 0 |
分析 (1)由表中數據列關于ω、φ的二元一次方程組,求得A、ω、φ的值,得到函數解析式,進一步完成數據補充.
(2)根據函數y=Asin(ωx+φ)的圖象變換規律可求g(x),利用正弦函數的性質可求其值域.
(3)由(1)及函數y=Asin(ωx+φ)的圖象變換規律得g(x),令2x+2θ+$\frac{π}{6}$=kπ,解得x=$\frac{kπ}{2}-\frac{π}{12}$-θ,k∈Z.令:$\frac{kπ}{2}-\frac{π}{12}$-θ=$\frac{π}{12}$,結合θ>0即可解得θ的最小值.
解答 解:(1)根據表中已知數據,解得A=3,ω=2,φ=$\frac{π}{6}$,
數據補全如下表:
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | -$\frac{π}{12}$ | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{2π}{3}$ | $\frac{11π}{12}$ |
| f(x) | 0 | 3 | 0 | -3 | 0 |
點評 本題考查了由y=Asin(ωx+φ)的部分圖象求解函數解析式,函數y=Asin(ωx+φ)的圖象變換規律的應用,考查了正弦函數的圖象和性質的應用,其中關鍵是要根據圖象分析出函數的最值,周期等,進而求出A,ω和φ值,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 19 | B. | 27 | C. | 28 | D. | 37 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 單位 | A1 | A2 | A3 | A4 | A5 |
| 平均身高x(單位:cm) | 170 | 174 | 176 | 181 | 179 |
| 平均得分y | 62 | 64 | 66 | 70 | 68 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
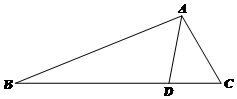 如圖,在△ABC中,D是BC上的點,AC=3,CD=2,AD=$\sqrt{7}$,sinB=$\frac{\sqrt{7}}{7}$.
如圖,在△ABC中,D是BC上的點,AC=3,CD=2,AD=$\sqrt{7}$,sinB=$\frac{\sqrt{7}}{7}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com