
分析 (1)根據向量的模的定義和二次函數的性質即可求出,
(2)根據$\overrightarrow{a}$=2$\overrightarrow{b}$,結合三角函數的恒等變換,求出m的取值范圍,再求$\frac{λ}{m}$的取值范圍即可.
解答 解:(1)當a=$\frac{π}{12}$時,$\overrightarrow{b}$=(m,$\frac{m}{2}$+$\frac{1}{4}$),
∴|$\overrightarrow{b}$|2=$\frac{5}{4}$m2+$\frac{m}{4}$+$\frac{1}{16}$=$\frac{5}{4}$(m2+$\frac{1}{5}$m)+$\frac{1}{16}$=$\frac{5}{4}$(m+$\frac{1}{10}$)2+$\frac{1}{20}$,
∴|$\overrightarrow{b}$|=$\frac{\sqrt{5}}{10}$
(2)∵$\overrightarrow{a}$=2$\overrightarrow{b}$,向量$\overrightarrow{a}$=(λ+2,λ2-$\sqrt{3}$cos2α),$\overrightarrow{b}$=(m,$\frac{m}{2}$+sinαcosα),
∴λ+2=2m,λ2-$\sqrt{3}$cos2α=m+sin2α
∴4m2-9m+4=sin2α+$\sqrt{3}$cos2α=2sin(2α+$\frac{π}{3}$),
∵-2≤2sin(2α+$\frac{π}{3}$)≤2,
∴-2≤4m2-9m+4≤2,
解得$\frac{1}{4}$≤m≤2
而$\frac{λ}{m}$=2-$\frac{2}{m}$,
∴$\frac{λ}{m}$∈[-6,1]
點評 本題考查了平面向量的應用問題,也考查了三角恒等變換的應用問題,還考查了求函數的最值問題,是綜合題.


 智慧小復習系列答案
智慧小復習系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 三角形 | B. | 正方形 | ||
| C. | 非正方形的長方形 | D. | 非正方形的菱形 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,在四棱錐P-ABCD中,底面ABCD是邊長為1的菱形,∠BAD=60°,側棱PA⊥底面ABCD,E、F分別是PA、PC的中點.
如圖,在四棱錐P-ABCD中,底面ABCD是邊長為1的菱形,∠BAD=60°,側棱PA⊥底面ABCD,E、F分別是PA、PC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
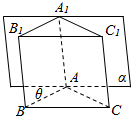 已知在直三棱柱ABC-A1B1C1中,∠BAC=120°,AB=AC=1,AA1=2,若棱AA1在正視圖的投影面α內,且AB與投影面α所成角為θ(30°≤θ≤60°),設正視圖的面積為m,側視圖的面積為n,當θ變化時,mn的最大值是( )
已知在直三棱柱ABC-A1B1C1中,∠BAC=120°,AB=AC=1,AA1=2,若棱AA1在正視圖的投影面α內,且AB與投影面α所成角為θ(30°≤θ≤60°),設正視圖的面積為m,側視圖的面積為n,當θ變化時,mn的最大值是( )| A. | 2$\sqrt{3}$ | B. | 4 | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{3}{4}$ | B. | $\frac{5}{4}$ | C. | $\frac{7}{4}$ | D. | $\frac{9}{4}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com