
分析 若不等式xy≤ax2+2y2恒成立,則a≥-2($\frac{y}{x}$)2+$\frac{y}{x}$恒成立,令t=$\frac{y}{x}$,結合二次函數的圖象和性質,求得函數的最值,可得答案.
解答 解:若不等式xy≤ax2+2y2恒成立,
則a≥-2($\frac{y}{x}$)2+$\frac{y}{x}$恒成立,
令t=$\frac{y}{x}$,x∈[2,4],y∈[2,3],則t∈[$\frac{1}{2}$,$\frac{3}{2}$],
則u=-2($\frac{y}{x}$)2+$\frac{y}{x}$=-2t2+t在[$\frac{1}{2}$,$\frac{3}{2}$]上為減函數,
當t=$\frac{1}{2}$時,u取最大值0,
故a≥0,
故答案為:a≥0
點評 本題考查的知識點是恒成立問題,二次函數的圖象和性質,函數的最值及其幾何意義,難度中檔.


 王后雄學案教材完全解讀系列答案
王后雄學案教材完全解讀系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
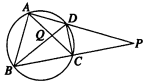 如圖所示,圓內接四邊形ABCD的一組對邊AD,BC的延長線相交于點P,對角線AC,BD相交于點Q,則圖中相似三角形共有( )
如圖所示,圓內接四邊形ABCD的一組對邊AD,BC的延長線相交于點P,對角線AC,BD相交于點Q,則圖中相似三角形共有( )| A. | 4對 | B. | 2對 | C. | 5對 | D. | 3對 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $y=-{x^{\frac{1}{2}}}$ | B. | y=-x2+|x| | C. | y=ln|x| | D. | y=-x2+x |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com