
| A. | 6 | B. | 10 | C. | 12 | D. | 18 |
分析 畫出可行域表示的平面區域,找出最優解,求出目標函數的最小值.
解答 解:畫出可行域$\left\{\begin{array}{l}{2x+y-6≥0}\\{x+2y-6≥0}\\{y≥0}\end{array}\right.$表示的平面區域,如圖所示;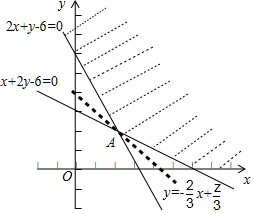
由$\left\{\begin{array}{l}{2x+y-6=0}\\{x+2y-6=0}\end{array}\right.$求得點A(2,2),
目標函數z=2x+3y化為y=-$\frac{2}{3}$x+$\frac{z}{3}$;
當目標函數過點A時,z取得最小值為
zmin=2×2+3×2=10.
故選:B.
點評 本題考查了簡單的線性規劃的應用問題,也考查了數形結合的應用問題,是基礎題.


科目:高中數學 來源: 題型:選擇題
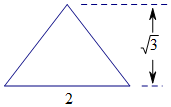 一個四棱錐的側棱長都相等,底面是正方形,且其正視圖為如圖所示的等腰三角形,則該四棱錐的體積是( )
一個四棱錐的側棱長都相等,底面是正方形,且其正視圖為如圖所示的等腰三角形,則該四棱錐的體積是( )| A. | $\frac{{4\sqrt{3}}}{3}$ | B. | $2\sqrt{3}$ | C. | $4\sqrt{3}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $y=x+\frac{4}{x}$ | B. | $y=sinx+\frac{4}{sinx}(0<x<π)$ | ||
| C. | y=4log3x+logx3 | D. | y=4ex+e-x |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | m<-1 | B. | m≥$\frac{2\sqrt{3}}{3}$ | C. | m≤-$\frac{2\sqrt{3}}{3}$ | D. | m≥$\frac{2\sqrt{3}}{3}$或m≤-$\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com