Question

13．已知函數f（x）=$\frac{a+lnx}{x}$在點（1，f（1））處的切線與x軸平行．
（1）求實數a的值及f（x）的極值；
（2）是否存在區間$（t，t+\frac{2}{3}）$（t＞0），使得f（x）在此區間上存在極值點和零點？若存在，求出實數t的取值范圍，若不存在，請說明理由；
（3）如果對任意x₁、x₂∈[e²，+∞]，有|f（x₁）-f（x₂）|≥k|$\frac{1}{x_1}-\frac{1}{x_2}$|，求實數k的取值范圍．

Answer 1

分析 （1）由函數f（x）在（1，f（1））處的切線與x軸平行求得a的值，然后利用函數的導函數的符號求出函數的單調期間，則函數的極值可求；
（2）假設存在區間（t，t+$\frac{2}{3}$）（t＞0），使函數f（x）在此區間上存在極值和零點，則得到關于t的不等式組，解此不等式組求得t的取值范圍；
（3）由（I）的結論知，f（x）在[e²，+∞）上單調遞減，然后構造函數F（x）=f（x）-$\frac{k}{x}$，由函數在[e²，+∞）上單調遞減，則其導函數在在[e²，+∞）上恒成立，由此求得實數k的取值范圍．

解答 解：（1）由f（x）=$\frac{a+lnx}{x}$，得f′（x）=$\frac{1-a-lnx}{{x}^{2}}$，
∵f（x）在點（1，f（1））處的切線與x軸平行，
∴f′（1）=$\frac{1-a-ln1}{{1}^{2}}$=0，∴a=1，
∴f（x）=$\frac{1+lnx}{x}$，x＞0，f′（x）=-$\frac{lnx}{{x}^{2}}$，
當0＜x＜1時，f′（x）＞0，當x＞1時，f′（x）＜0．
∴f（x）在（0，1）上單調遞增，在（1，+∞）單調遞減，
故f（x）在x=1處取得極大值1，無極小值；
（2）∵x＞1時，f（x）=$\frac{1+lnx}{x}$＞0，
當x→0時，y→-∞，
由（I）得f（x）在（0，1）上單調遞增，
∴由零點存在原理，f（x）在區間（0，1）存在唯一零點，函數f（x）的圖象如圖所示：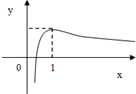

∵函數f（x）在區間（t，t+$\frac{2}{3}$），t＞0上存在極值和零點．
∴$\left\{\begin{array}{l}{0＜t＜1＜t+\frac{2}{3}}\\{f（t）=\frac{1+lnt}{t}＜0}\end{array}\right.$，解得$\frac{1}{3}$＜t＜$\frac{1}{e}$
∴存在符合條件的區間，實數t的取值范圍為（$\frac{1}{3}$，$\frac{1}{e}$）；
（3）由（1）的結論知，f（x）在[e²，+∞）上單調遞減，
不妨設x1＞x2≥e2，則|f（x₁）-f（x₂）|≥k|$\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$|，
則f（x₂）-f（x₁）≥k（$\frac{1}{{x}_{2}}$-$\frac{1}{{x}_{1}}$），
∴f（x₂）-$\frac{k}{{x}_{2}}$≥f（x₁）-$\frac{k}{{x}_{1}}$，
∴函數F（x）=f（x）-$\frac{k}{x}$在[e²，+∞）上單調遞減，
又F（x）=f（x）-$\frac{k}{x}$=$\frac{1+lnx}{x}$-$\frac{k}{x}$，
∴F′（x）=$\frac{k-lnx}{{x}^{2}}$≤0在[e²，+∞）上恒成立，
∴k≤lnx在[e²，+∞）上恒成立．
在[e²，+∞）上（lnx）_min=lne²=2，
∴k≤2．

點評 本題考查了利用導數研究過曲線上某點處的切線方程，考查了利用導數求函數的最值，訓練了函數零點的判定方法，訓練了利用恒成立問題求參數的范圍，綜合考查了學生的邏輯思維能力和計算能力，是壓軸題．