
分析 聯立兩曲線方程,可得tanx=$\frac{sinx}{cosx}$=$\frac{a}{2}$,a>0,設交點P(m,n),分別求出f(x),g(x)的導數,可得切線的斜率,由兩直線垂直的條件:斜率之積為-1,再由同角基本關系式,化弦為切,解方程即可得到a的值.
解答 解:由f(x)=g(x),即2sinx=acosx,
即有tanx=$\frac{sinx}{cosx}$=$\frac{a}{2}$,a>0,
設交點P(m,n),
f(x)=2sinx的導數為f′(x)=2cosx,
g(x)=acosx的導數為g′(x)=-asinx,
由兩曲線在點P處的切線互相垂直,
可得2cosm•(-asinm)=-1,
且tanm=$\frac{a}{2}$,
則$\frac{2asinmcosm}{si{n}^{2}m+co{s}^{2}m}$=1,
分子分母同除以cos2m,
即有$\frac{2atanm}{1+ta{n}^{2}m}$=1,
即為a2=1+$\frac{{a}^{2}}{4}$,
解得a=$\frac{{2\sqrt{3}}}{3}$.
故答案為:$\frac{{2\sqrt{3}}}{3}$.
點評 本題考查導數的運用:求切線的斜率,兩直線垂直的條件:斜率之積為-1,同時考查同角三角函數的基本關系式,考查化簡整理的運算能力,屬于中檔題.


 手拉手全優練考卷系列答案
手拉手全優練考卷系列答案科目:高中數學 來源: 題型:選擇題
| A. | $4+2\sqrt{2}$ | B. | $4\sqrt{2}$ | C. | $3+2\sqrt{2}$ | D. | $3+\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
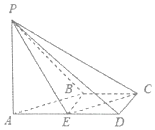 如圖,在四棱錐P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD.E為棱AD的中點,異面直線PA與CD所成的角為90°.
如圖,在四棱錐P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD.E為棱AD的中點,異面直線PA與CD所成的角為90°.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-1,1) | B. | (-1,0) | C. | {-1,0,1} | D. | {-1,0} |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com