
| A. | 5個 | B. | 4個 | C. | 3個 | D. | 2個 |
分析 由題意可得求函數y=f(|x|)的圖象和直線y=a的交點個數.作出函數y=f(|x|)的圖象,平移直線y=a,即可得到所求交點個數,進而得到結論
解答  解:函數f(x)=$\left\{\begin{array}{l}{log_2}(1-x),x<1\\-{(x-2)^2}+2,x≥1\end{array}$,方程f(|x|)=a,(a∈R)實根個數,
解:函數f(x)=$\left\{\begin{array}{l}{log_2}(1-x),x<1\\-{(x-2)^2}+2,x≥1\end{array}$,方程f(|x|)=a,(a∈R)實根個數,
即為函數y=f(|x|)和直線y=a的交點個數.
由y=f(|x|)為偶函數,可得圖象關于y軸對稱.
作出函數y=f(|x|)的圖象,如圖,
平移直線y=a,可得它們有2個、3個、4個交點.
不可能有5個交點,即不可能有5個實根,
故選:A.
點評 本題考查方程的實根個數問題的解法,注意運用轉化思想和數形結合的方法,考查判斷和作圖能力,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{4}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{x^2}{9}-\frac{y^2}{16}=1$ | B. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | C. | $\frac{x^2}{3}-\frac{y^2}{4}=1$ | D. | $\frac{x^2}{4}-\frac{y^2}{3}=1$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a<b<c | B. | b<c<a | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
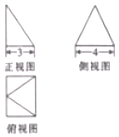 某幾何體的三視圖如圖所示,其側視圖是一個等邊三角形,則此幾何體的體積是( )
某幾何體的三視圖如圖所示,其側視圖是一個等邊三角形,則此幾何體的體積是( )| A. | 24$\sqrt{3}$ | B. | 8$\sqrt{3}$ | C. | 16$\sqrt{3}$ | D. | 16 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com