
| A. | $\frac{11}{12}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{6}$ | D. | $\frac{5}{6}$ |
分析 (1)由題意知本題是一個古典概型,事件(a,b)的基本事件有36個,方程組只有一個解,需滿足2b-4a≠0,即b≠2a,而b=2a的事件有(1,2),(2,4),(3,6)共3個,根據古典概型概率公式得到結果
解答 解:(1)由題意知本題是一個古典概型,
事件(a,b)的基本事件有36個.
由方程組$\left\{\begin{array}{l}{ax+by=3}\\{2x+4y=7}\end{array}\right.$
可得$\left\{\begin{array}{l}{(2b-4a)x=8b-12}\\{(2b-4a)y=6-7a}\end{array}\right.$
方程組只有一個解,需滿足2b-4a≠0,
即b≠2a,而b=2a的事件有(1,2),(2,4),(3,6)共3個,
所以方程組只有一個解的概率為P1=1-$\frac{3}{36}$=$\frac{11}{12}$,
故選A.
點評 本題考查古典概型,考查解方程組,是一個綜合題,概率問題往往同其他的知識點結合在一起,實際上是以概率問題為載體,主要考查的是另一個知識點


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 已知函數f(x)=$\left\{\begin{array}{l}-\frac{1}{2}{x^2}-2x({x≤0})\\{(\frac{1}{2})^x}+1({x>0})\end{array}$.
已知函數f(x)=$\left\{\begin{array}{l}-\frac{1}{2}{x^2}-2x({x≤0})\\{(\frac{1}{2})^x}+1({x>0})\end{array}$.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,0) | B. | (0,1) | C. | (1,2) | D. | (2,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
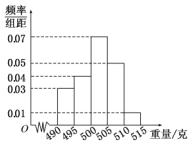 某食品廠為了檢查一條自動包裝流水線的生產情況,隨機抽取該流水線上40件產品作為樣本稱出它們的重量(單位:克),重量的分組區間為 (490,495],(495,500],…,(510,515],由此得到樣本的頻率分布直方圖,如圖所示.
某食品廠為了檢查一條自動包裝流水線的生產情況,隨機抽取該流水線上40件產品作為樣本稱出它們的重量(單位:克),重量的分組區間為 (490,495],(495,500],…,(510,515],由此得到樣本的頻率分布直方圖,如圖所示.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com