
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 $f(x)=\sqrt{{x^2}+4x+5}+\sqrt{{x^2}-2x+10}$表示x軸上點P(x,0)到點A((-2,-1)、B(1,3)的距離之和,因為點A、B在x軸的兩側,距離之和的最小值就是A、B的距離.
解答 解:函數$f(x)=\sqrt{{x^2}+4x+5}+\sqrt{{x^2}-2x+10}$表示x軸上點P(x,0)到點A((-2,-1)、B(1,3)的距離之和,因為點A、B在x軸的兩側,距離之和的最小值就是A、B的距離,且AB=$\sqrt{(-2-1)^{2}+(-1-3)^{2}}\\;\\;=5$=5.
故答案選C
點評 本題考查了函數表達式的幾何意義,把函數的最值轉化為點的距離,利用數形結合求解,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | {x|-2<x<5} | B. | {x|2<x<5} | C. | {x|2≤x≤7} | D. | {x|-2≤x≤7} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
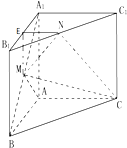 如圖,在直三棱柱ABC-A1B1C1中,AB⊥AC,點M、N、E分別為A1B、B1C1、A1B1上的中點.
如圖,在直三棱柱ABC-A1B1C1中,AB⊥AC,點M、N、E分別為A1B、B1C1、A1B1上的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | m=1,且f(x)在(0,1)上是增函數 | B. | m=1,且f(x)在(0,1)上是減函數 | ||
| C. | m=-1,且f(x)在(0,1)上是增函數 | D. | m=-1,且f(x)在(0,1)上是減函數 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a≤0 | B. | $a>\frac{1}{2}$ | C. | a≥0 | D. | $a<\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com