
分析 (1)將函數f(x)化簡,圖象上的一個最高點為($\frac{π}{6}$,1),可得C的值,與其相鄰的最低點是($\frac{2π}{3}$,-3).可得周期.從而得到f(x)的解析式.根據三角函數的圖象及性質可得對稱中心;
(2)$\overrightarrow{AB}$•$\overrightarrow{BC}$=-$\frac{1}{2}$ac,利用夾角公式,可得cosB的值,即B的值,利用f(x)的解析式可求解.
解答 解:(1)函數f(x)=$\sqrt{3}$sinωx+cosωx+c(ω>0,x∈R,c是常數)
化簡得:f(x)=2sin(ωx+$\frac{π}{6}$)+c;
∵2sin(ωx+$\frac{π}{6}$)∈[-1,1],即f(x)的最大值為2+c.
函數f(x)圖象上的一個最高點為縱坐標為1,即最大值為1,
則有:2+c=1,解得:c=-1.
∵最高點為($\frac{π}{6}$,1),與其相鄰的最低點為($\frac{2π}{3}$,-3).
∴$\frac{1}{2}T=\frac{2π}{3}-\frac{π}{6}$,
解得:T=π,
∵T=$\frac{2π}{ω}=π$,
∴ω=2
故得:函數f(x)=2sin(2x+$\frac{π}{6}$)-1;
對稱中心:2x+$\frac{π}{6}$=kπ,(k∈Z)
解得:x=$\frac{1}{2}kπ-\frac{π}{12}$.
故得:函數f(x)的對稱中心坐標為($\frac{1}{2}kπ-\frac{π}{12}$,-1)(k∈Z).
(2)由(1)可得函數f(A)=2sin(2A+$\frac{π}{6}$)-1;
∵$\overrightarrow{AB}$•$\overrightarrow{BC}$=-$\frac{1}{2}$ac,$\overrightarrow{AB}•\overrightarrow{BC}=|\overrightarrow{AB}|•|\overrightarrow{BC}|•COSB$,
∴-ac•cosB=-$\frac{1}{2}$ac,
可得:cosB=$\frac{1}{2}$,
故得:B=$\frac{π}{3}$.
∴A∈(0,$\frac{2π}{3}$)
2A+$\frac{π}{6}$∈($\frac{π}{6}$,$\frac{3π}{2}$),
∴函數f(A)=2sin(2A+$\frac{π}{6}$)-1的值域(-3,1].
即函數f(A)的取值范圍是(-3,1].
點評 本題考查了三角函數的化簡能力和性質的綜合運用能力,向量的夾角公式的運用.屬于中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [-2$\sqrt{3}$-4,-2$\sqrt{3}$+4] | B. | (-∞,-2$\sqrt{3}$-4]∪[-2$\sqrt{3}$+4,+∞) | ||
| C. | [-2$\sqrt{3}$+4,+∞) | D. | (-∞,-$\frac{1}{2}$] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 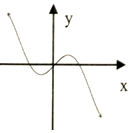 | B. |  | C. | 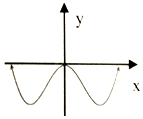 | D. | 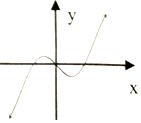 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 10 | B. | $\frac{1}{10}$ | C. | 100 | D. | $\frac{1}{100}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | am+1<am+2 | B. | am+1>bm+2 | C. | bm+2<am+2 | D. | bm+1>bm+2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com