
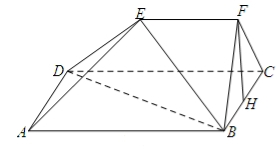
如圖,在五面體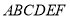 中,四邊形
中,四邊形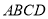 是邊長為
是邊長為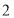 的正方形,
的正方形,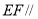 平面
平面 ,
,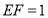 ,
,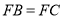 ,
,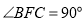 ,
,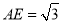 ,
,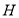 是
是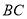 的中點.
的中點.
(1)求證: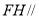 平面
平面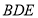 ;
;
(2)求證: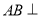 平面
平面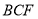 ;
;
(3)求五面體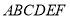 的體積.
的體積.
(1)詳見解析;(2)詳見解析;(3)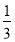 .
.
【解析】
試題分析:(1)連接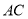 交
交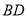 于點
于點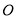 ,取
,取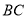 的中點
的中點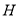 ,連接
,連接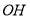 、
、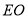 ,先證明
,先證明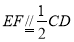 ,再利用中位線證明
,再利用中位線證明 ,利用傳遞性證明
,利用傳遞性證明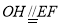 ,進而證明四邊形
,進而證明四邊形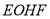 為平行四邊形,進而得到
為平行四邊形,進而得到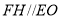 ,最后利用直線與平面平行的判定定理證明
,最后利用直線與平面平行的判定定理證明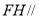 平面
平面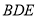 ;(2)證法一是取
;(2)證法一是取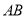 的中點
的中點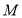 ,先證明四邊形
,先證明四邊形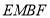 為平行四邊形得到
為平行四邊形得到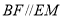 ,然后通過勾股定理證明
,然后通過勾股定理證明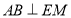 從而得到
從而得到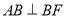 ,然后結合四邊形
,然后結合四邊形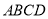 為正方形得到
為正方形得到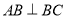 ,最后利用直線與平面垂直的判定定理證明
,最后利用直線與平面垂直的判定定理證明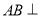 平面
平面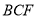 ;證法二是連接
;證法二是連接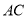 交
交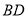 于點
于點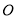 ,先利用勾股定理證明
,先利用勾股定理證明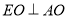 ,利用
,利用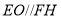 得到
得到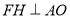 ,再利用等腰三角形
,再利用等腰三角形 中三線合一得到
中三線合一得到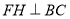 ,利用直線與平面垂直的判定定理證明
,利用直線與平面垂直的判定定理證明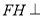 平面
平面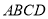 ,進而得到
,進而得到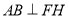 ,然后結合四邊形
,然后結合四邊形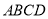 為正方形得到
為正方形得到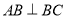 ,最后利用直線與平面垂直的判定定理證明
,最后利用直線與平面垂直的判定定理證明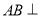 平面
平面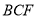 ;(3)將五面體分割為四棱錐
;(3)將五面體分割為四棱錐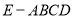 與三棱錐
與三棱錐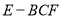 ,利用(2)中的結論
,利用(2)中的結論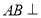 平面
平面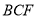 得到
得到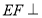 平面
平面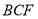 從而計算三棱錐
從而計算三棱錐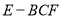 的體積,利用結論
的體積,利用結論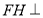 平面
平面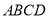 以及
以及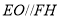 得到
得到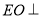 平面
平面 以此計算四棱錐
以此計算四棱錐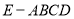 的體積,最終將兩個錐體的體積相加得到五面體
的體積,最終將兩個錐體的體積相加得到五面體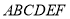 的體積.
的體積.
試題解析:(1)連接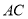 ,
,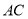 與
與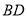 相交于點
相交于點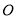 ,則
,則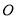 是
是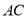 的中點,連接
的中點,連接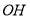 、
、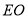 ,
,
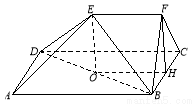
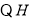 是
是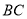 的中點,
的中點,
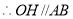 ,
,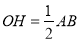 ,
,
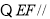 平面
平面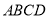 ,
,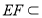 平面
平面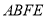 ,平面
,平面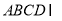 平面
平面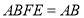 ,
,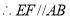 ,
,
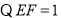 ,
,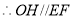 ,
,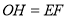 ,
, 四邊形
四邊形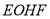 為平行四邊形,
為平行四邊形,
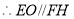 ,
,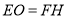 ,
,
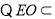 平面
平面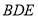 ,
,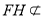 平面
平面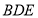 ,
,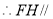 平面
平面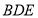 ;
;
(2)證法1:取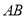 的中點
的中點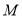 ,連接
,連接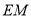 ,則
,則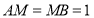 ,
,

由(1)知,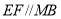 ,且
,且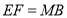 ,
, 四邊形
四邊形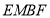 為平行四邊形,
為平行四邊形,
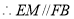 ,
,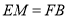 ,
,
在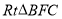 中,
中,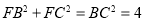 ,又
,又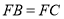 ,得
,得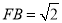 ,
,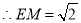 ,
,
在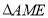 中,
中,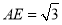 ,
,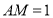 ,
,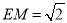 ,
,
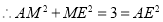 ,
,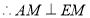 ,
,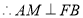 ,即
,即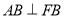 ,
,
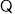 四邊形
四邊形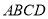 是正方形,
是正方形,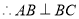 ,
,
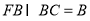 ,
,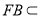 平面
平面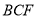 ,
,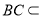 平面
平面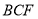 ,
,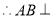 平面
平面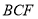 ;
;
證法2:在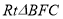 中,
中,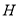 為
為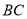 的中點,
的中點,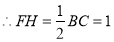 .
.
在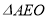 中,
中,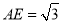 ,
,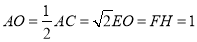 ,
,
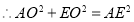 ,
,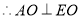 ,
,
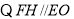 ,
,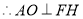 ,
,
 ,
,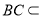 平面
平面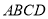 ,
,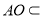 平面
平面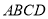 ,
,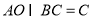 ,
,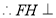 平面
平面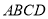 ,
,
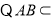 平面
平面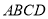 ,
,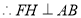 .
.
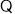 四邊形
四邊形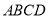 是正方形,
是正方形,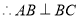 .
.
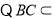 平面
平面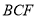 ,
,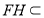 平面
平面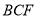 ,
,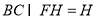 ,
,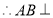 平面
平面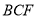 .
.

(3)連接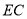 ,
,
在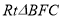 中,
中,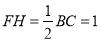 ,
,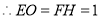 .
.
由(2)知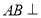 平面
平面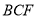 ,且
,且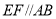 ,
,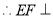 平面
平面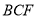 .
.
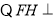 平面
平面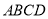 ,
,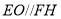 ,
,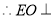 平面
平面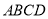 .
.
 四棱錐
四棱錐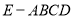 的體積為
的體積為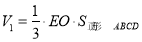
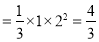 .
.
 三棱錐
三棱錐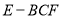 的體積為
的體積為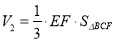
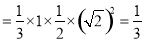 .
.
 五面體
五面體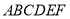 的體積為
的體積為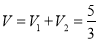 .
.
考點:1.直線與平面平行;2直線與平面垂直;3.分割法求多面體的體積


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:2013-2014學年廣東省揭陽市高三3月第一次模擬考試理科數學試卷(解析版) 題型:選擇題
下列函數是偶函數,且在 上單調遞增的是( )
上單調遞增的是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東省惠州市高三4月模擬考試文科數學試卷(解析版) 題型:選擇題
如圖,一個空間幾何體的主視圖、左視圖、俯視圖為全等的等腰直角三角形,如果 直角三角形的直角邊長為
直角三角形的直角邊長為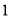 ,那么這個幾何體的體積為 ( )
,那么這個幾何體的體積為 ( )

A.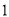 B.
B.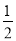 C.
C.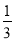 D.
D.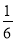
查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東省廣州市畢業班綜合測試二文科數學試卷(解析版) 題型:選擇題
一個幾何體的三視圖如圖所示,則該幾何體的體積為( )
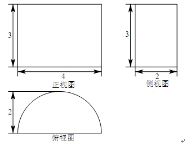
A.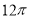 B.
B.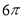 C.
C.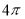 D.
D.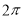
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com