
分析 形如f(m+n)=f(m)+f(n)-2的函數模型,實際上是一次函數f(x)=kx+b的抽象.第(1)小問結合已知先構造x2-x1>0,可得f(x2-x1)>2,利用函數的單調性的定義作差f(x1)-f(x2)變形可證明.
(2)由f(-3)=-7 及由已知不等式及函數的單調性可轉化原不等式,結合恒成立與最值求解的相互轉化即可求解.
解答 (1)證明:(Ⅰ)?x1,x2∈R,當x1<x2時,x2-x1>0,∴f(x2-x1)>2,
則f(x1)-f(x2)
=f(x1)-f(x2-x1+x1)
=f(x1)-f(x2-x1)-f(x1)+2
=2-f(x2-x1)<0,
所以f(x1)<f(x2),
所以f(x)在R上是單調遞增函數.
(2)∵f(-3)=-7,∴不等式f(t2+at-a)≥-7對任意t∈[-2,2]恒成立,⇒f(t2+at-a)≥f(-3)對任意t∈[-2,2]恒成立
∵f(x)在R上是單調遞增函數,所以t2+at-a≥-3⇒t2+at-a+3≥0對任意t∈[-2,2]恒成立.
記g(t)=t2+at-a+3(-2≤t≤2)
只需g(t)min≥0.對稱軸t=-$\frac{a}{2}$,
1)當$-\frac{a}{2}$≤-2時,即a≥4時g(t)min=g(-2)=4-3a+3≥0,a$≤\frac{7}{3}$ 與a≥4矛盾.此時a∈ϕ;
2)當-2$<\frac{a}{2}<2$,即-4<a<4時,g(t)min=g(-$\frac{a}{2}$≥0,所以-4<a≤2;
3)當$\frac{a}{2}≥2$時,即a>4時,gmin(t)=g(2)=4+2a-a+3≥0⇒a≥-7,又a≤-4,∴-7≤a≤-4;
綜合上述得:a∈[-7,2].
點評 本題主要考查了抽象函數的單調性的證明及解抽象函數函數的恒成立問題的處理方法,具有很強的綜合性,屬于中檔題.


科目:高中數學 來源: 題型:填空題

查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $(0,\frac{{\sqrt{3}}}{3}]$ | B. | $(0,\frac{{\sqrt{3}}}{3}]∪$(1,+∞) | C. | $[\frac{{\sqrt{3}}}{3},1)$ | D. | (1,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
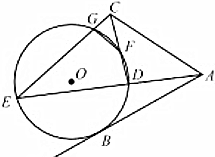 如圖,AB是圓O的一條切線,切點為B,直線ABD,CFD,CGE都是圓O的割線,已知AC=AB.
如圖,AB是圓O的一條切線,切點為B,直線ABD,CFD,CGE都是圓O的割線,已知AC=AB.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com