
| A. | ① | B. | ② | C. | ③ | D. | ④ |
分析 判斷方程${{x}_{\;}}^{2}+2{x}_{\;}+3=0$的實根個數,可判斷①;寫出原命題的否定命題,可判斷②;舉出反例a=1,b=-1,可判斷③; 根據互為逆否的兩個命題真假性相同,可判斷④.
解答 解:方程${{x}_{\;}}^{2}+2{x}_{\;}+3=0$的△=4-12<0,故方程無實根,
故①?x0∈R,使${x_0}^2+2{x_0}+3=0$為假命題;
②命題“?x0∈R,lgx0>0”的否定是“?x∈R,lgx≤0”,故②為假命題;
③如果a=1,b=-1∈R,則a>b,但a2=b2,故③為假命題;
④“若α=β,則sinα=sinβ”為真命題,故其逆否命題為真命題,故④為真命題.
故選:D
點評 本題以命題的真假判斷與應用為載體,考查了特稱命題,方程根的存在性及個數判斷,不等式與不等關系,三角函數的定義等知識點,難度中檔.


科目:高中數學 來源: 題型:解答題
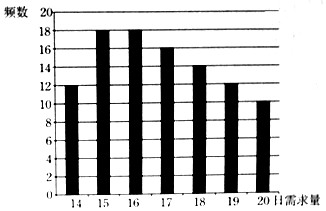 某蛋糕店每天制作生日蛋糕若干個,每個生日蛋糕成本為50元,每個蛋糕的售價為100元,如果當天賣不完,剩余的蛋糕作垃圾處理.現搜集并整理了100天生日蛋糕的日需求量(單位:個),得到如圖所示的柱狀圖.100天記錄的各需求量的頻率作為每天各需求量發生的概率.
某蛋糕店每天制作生日蛋糕若干個,每個生日蛋糕成本為50元,每個蛋糕的售價為100元,如果當天賣不完,剩余的蛋糕作垃圾處理.現搜集并整理了100天生日蛋糕的日需求量(單位:個),得到如圖所示的柱狀圖.100天記錄的各需求量的頻率作為每天各需求量發生的概率.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
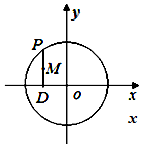 如圖,在圓x2+y2=16上任取一點P,過點P作x 軸的垂線段PD,D為垂足,當點P在圓上運動時,則線段PD的中點M的軌跡方程為$\frac{x^2}{16}+\frac{y^2}{4}=1$.
如圖,在圓x2+y2=16上任取一點P,過點P作x 軸的垂線段PD,D為垂足,當點P在圓上運動時,則線段PD的中點M的軌跡方程為$\frac{x^2}{16}+\frac{y^2}{4}=1$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
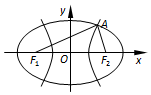 如圖,F1,F2是橢圓C1與雙曲線C2的公共焦點,點A是C1,C2的公共點.設C1,C2的離心率分別是e1,e2,∠F1AF2=2θ,則( )
如圖,F1,F2是橢圓C1與雙曲線C2的公共焦點,點A是C1,C2的公共點.設C1,C2的離心率分別是e1,e2,∠F1AF2=2θ,則( )| A. | ${e_1}^2{sin^2}θ+{e_2}^2{cos^2}θ=e_1^2e_2^2$ | |
| B. | ${e_2}^2{sin^2}θ+{e_1}^2{cos^2}θ=e_1^2e_2^2$ | |
| C. | ${e_2}^2{sin^2}θ+{e_1}^2{cos^2}θ=1$ | |
| D. | ${e_1}^2{sin^2}θ+{e_2}^2{cos^2}θ=1$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com