Question

4．為打擊索馬里海盜，保護各國商船的順利通行，我海軍某部奉命前往該海域執行護航任務，某天我護航艦正在某小島A北偏西45°并距該島20海里的B處待命，位于該島正西方向C處的某外國商船遭到海盜襲擊，船長發現在其北偏東60°的方向有我軍護航艦（如圖所示），便發出緊急求救信號，我護航艦接警后，立即沿BC航線以每小時60海里的速度前去救援，問我護航艦需多少分鐘可以到達該商船所在的位置C處？（結果精確到個位，參考數據：$\sqrt{2}$≈1.4，$\sqrt{3}$≈1.7）

Answer 1

分析 由條件可知△ABC為斜三角形，所以作AC上的高，轉化為兩個直角三角形求解．

解答 （本題滿分為6分）
解：由圖可知，∠ACB=30°，∠BAC=45°． （1分）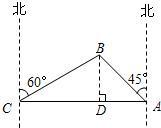
作BD⊥AC于D（如圖）．
在Rt△ADB中，AB=20，
∴BD=AB•sin45°=20×$\frac{\sqrt{2}}{2}$=10$\sqrt{2}$．]（2分）
在Rt△BDC中，∠ACB=30°，
∴BC=2×10$\sqrt{2}$=20$\sqrt{2}$≈28.\（3分）
∴$\frac{28}{60}$≈0.47． （4分）
∴0.47×60=28.2≈28（分鐘）．5分）
答：我護航艦約需28分鐘就可到達該商船所在的位置C．（6分）

點評 本題主要考查了解三角形中的實際應用，化斜為直是解三角形的基本思路，考查了數形結合思想，屬于中檔題．